Теорема о приведении системы сил к данному центру

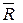Теорем. Любая система сил, действующих на абсолютно твердое тело, при приведении к произвольно выбранному центру О заменяется одной силой , равной главному вектору системы сил и приложенной в центре приведения О, и одной парой с моментом 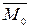, равным главному моменту системы сил относительно центра О.(рис.б)

Доказательство: Пусть на твердое тело действует произвольная система сил , , 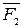… 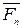(рис. а). Выберем какую-нибудь точку О за центр приведения и, пользуясь теоремой Пуансо, перенесем все силы в центр О, присоединяя при этом соответствующие пары. Тогда на тело будет действовать система сил

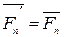, , … , (1)

приложенных в центре О, и система пар, моменты которых равны:

, , … , . (2)

Сходящиеся силы, приложенные в точке О, заменяются одной силой 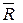, приложенной в точке О. При этом 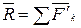или, согласно равенствам (1), .

Чтобы сложить все полученные пары, надо сложить векторы моментов этих пар. В результате система пар заменится одной парой, момент которой или, согласно равенствам (2), .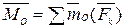

Величина 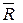, равная геометрической сумме всех сил, называется главным вектором системы сил; величина 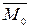, равная геометрической сумме моментов всех сил относительно центра О, называется главным моментом системы сил относительно этого центра. Теорема доказана.

Заметим, что сила 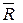не является здесь равнодействующей данной системы сил, так как заменяет систему сил не одна, а вместе с парой.

Cледcтвие. Две системы сил, имеющие одинаковые главные векторы и главные моменты относительно одного и того же центра, эквивалентны (условия эквивалентности систем сил).

Отметим еще, что значение 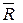от выбора центра О, очевидно, не зависит. Значение же 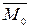при изменении положения центра О может в общем случае изменяться вследствие изменения значений моментов отдельных сил.