Расчет плоских ферм.
Расчет фермы сводится к определению опорных реакций и усилий в ее стержнях. Причем опорные реакции можно найти обычными методами статики, рассматривая ферму как твердое тело. Усилия в стержнях определяются с помощью метода вырезания узлов или метода Риттера (сечений).
1. Метод вырезания узлов. При этом методе мысленно вырезают узлы фермы и прикладывают к ним соответствующие внешние силы и реакции стержней и составляют уравнения равновесия сходящихся сил, приложенных к каждому узлу (  ,
, 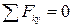 ). Условно предполагают, что все стержни растянуты, т.е реакция стержней направлены от узлов. Если в результате вычислений получат ответ со знаком минус, то это значит, что соответствующий стержень сжат. Последовательность рассмотрения узлов определяется обычно условием, что число неизвестных сил, приложенных к узлу, не должно превышать числа уравнений равновесия, т.е. двух. Если вычисления правильные, то многоугольники сил, приложенных к узлам, должны быть замкнутыми.
). Условно предполагают, что все стержни растянуты, т.е реакция стержней направлены от узлов. Если в результате вычислений получат ответ со знаком минус, то это значит, что соответствующий стержень сжат. Последовательность рассмотрения узлов определяется обычно условием, что число неизвестных сил, приложенных к узлу, не должно превышать числа уравнений равновесия, т.е. двух. Если вычисления правильные, то многоугольники сил, приложенных к узлам, должны быть замкнутыми.
2. Метод Риттера (сечений). Этим методом удобно пользоваться для определения усилий в отдельных стержнях фермы, в частности для проверочных расчетов. Идея метода состоит в том, что ферму разделяют на две части сечением, проходящим через три стержня, в которых (или в одном из которых) требуется определить усилия, и рассматривают равновесие одной из этих частей. Действие отброшенной части заменяют соответствующими силами, направляя их вдоль разрезанных стержней от узлов. Затем составляют уравнения моментов сил, действующих на рассматриваемую часть фермы, относительно точки пересечения двух рассеченных стержней, усилия в которых на данном этапе не определяются. Это точка пересечения называется точкой Риттера. Если точка Риттера находится в бесконечности, т.е. стержни параллельны, то составляют уравнение проекций сил, приложенных к рассматриваемой части фермы, на ось перпендикулярную этим параллельным стержням.
14. Момент силы относительно центра (как вектор)
 Рассмотрим силу
Рассмотрим силу  , приложенную к телу в точке А. Из некоторого центра О опустим перпендикуляр на линию действия силы
, приложенную к телу в точке А. Из некоторого центра О опустим перпендикуляр на линию действия силы  , длину
, длину 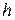 этого перпендикуляра называют плечом силы
этого перпендикуляра называют плечом силы  относительно центра О;
относительно центра О; 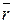 это радиус–вектор точки А, проведенный из точки О.
это радиус–вектор точки А, проведенный из точки О.
Определение. Моментом силы  относительно центра О называется приложенный в центре О вектор
относительно центра О называется приложенный в центре О вектор  , модуль которого равен произведению модуля F силы на ее плечо h и который направлен перпендикулярно плоскости, проходящей через центр О и силу, в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра О против хода часовой стрелки.
, модуль которого равен произведению модуля F силы на ее плечо h и который направлен перпендикулярно плоскости, проходящей через центр О и силу, в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра О против хода часовой стрелки.
Момент силы характеризует вращательный эффект силы. Согласно этому определению 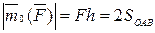 , т.к.
, т.к.  . Измеряется момент силы в ньютон·метрах (Н·м).
. Измеряется момент силы в ньютон·метрах (Н·м).
Найдем формулу, выражающую вектор  . Для этого рассмотрим векторное произведение
. Для этого рассмотрим векторное произведение  векторов
векторов  и
и  .
.
Векторным произведением 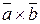 векторов
векторов 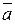 и
и  называется вектор
называется вектор  , равный по модулю площади параллелограмма, построенного на векторах
, равный по модулю площади параллелограмма, построенного на векторах 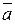 и
и  , и направленный перпендикулярно плоскости этих векторов в ту сторону, откуда кратчайшее совмещение
, и направленный перпендикулярно плоскости этих векторов в ту сторону, откуда кратчайшее совмещение 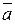 с
с  видно происходящим против хода часовой стрелки. Модуль
видно происходящим против хода часовой стрелки. Модуль 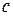 определяется еще равенством
определяется еще равенством 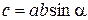 , где
, где 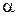 — угол между векторами
— угол между векторами 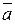 и
и  . Если векторы
. Если векторы 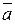 и
и  параллельны, то
параллельны, то 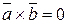 .
.
 .
.
Направлен вектор  перпендикулярно плоскости ОАВ в ту сторону, откуда кратчайшее совмещение
перпендикулярно плоскости ОАВ в ту сторону, откуда кратчайшее совмещение  с
с  (если их отложить от одной точки) видно происходящим против хода часовой стрелки, т. е. так же, как вектор
(если их отложить от одной точки) видно происходящим против хода часовой стрелки, т. е. так же, как вектор  . Следовательно, векторы
. Следовательно, векторы  и
и  совпадают и по модулю, и по направлению, и, как легко видеть, по размерности, т. е. выражают одну и ту же величину. Отсюда
совпадают и по модулю, и по направлению, и, как легко видеть, по размерности, т. е. выражают одну и ту же величину. Отсюда
 или
или 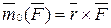 .
.
Таким образом, момент силы  относительно центра О равен векторному произведению радиуса-вектора
относительно центра О равен векторному произведению радиуса-вектора  , проведенного из центра О в точку А, где приложена сила, на саму силу.
, проведенного из центра О в точку А, где приложена сила, на саму силу.
Свойства момента силы: 1) момент силы относительно центра не изменяется при переносе точки приложения силы вдоль ее линии действия; 2) момент силы относительно центра О равен нулю или когда сила равна нулю, или когда линия действия силы проходит через центр О (плечо равно нулю).
 15. Момент силы относительно оси
15. Момент силы относительно оси
Проекция вектора 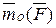 , т. е. момента силы
, т. е. момента силы  относительно центра О, на какую-нибудь ось z, проходящую через этот центр, называется моментом силы
относительно центра О, на какую-нибудь ось z, проходящую через этот центр, называется моментом силы  относительно оси z, т. е.
относительно оси z, т. е.
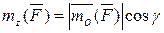
где  — момент силы
— момент силы  относительно оси z;
относительно оси z;  — угол между вектором
— угол между вектором 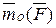 и осью z. Из определения следует, что
и осью z. Из определения следует, что  является величиной алгебраической.
является величиной алгебраической.
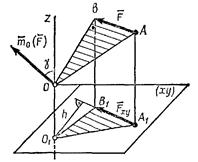
Проведем через произвольную точку 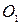 оси z (рис.) плоскость ху, перпендикулярную этой оси, и спроектируем
оси z (рис.) плоскость ху, перпендикулярную этой оси, и спроектируем  на эту плоскость. Так как вектор
на эту плоскость. Так как вектор 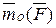 перпендикулярен плоскости ОАВ, а ось z перпендикулярна плоскости
перпендикулярен плоскости ОАВ, а ось z перпендикулярна плоскости 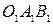 то угол
то угол  , как угол между нормалями к названным плоскостям, является углом между этими плоскостями. Т.е.
, как угол между нормалями к названным плоскостям, является углом между этими плоскостями. Т.е.  и
и
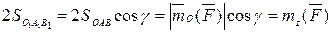
С другой стороны,  следовательно
следовательно

Таким образом, момент силы  относительно оси z равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную оси z, взятому относительно точки
относительно оси z равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную оси z, взятому относительно точки 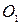 пересечения оси с этой плоскостью.
пересечения оси с этой плоскостью.
Момент силы относительно оси будет иметь знак плюс, когда с положительного конца оси поворот, который стремится совершить сила 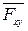 , виден происходящим против хода часовой стрелки, и знак минус — когда по ходу часовой стрелки.
, виден происходящим против хода часовой стрелки, и знак минус — когда по ходу часовой стрелки.
Чтобы вычислить момент силы относительно оси z, необходимо 
1) провести плоскость ху, перпендикулярную оси z (в любом месте); спроектировать силу  на эту плоскость и найти величину
на эту плоскость и найти величину  ;
;
2) опустить из точки пересечения оси с плоскостью (на рис. это точка О) перпендикуляр на линию действия 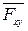 и найти его длину h;
и найти его длину h;
3) вычислить произведение 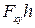 , и определить знак момента.
, и определить знак момента.
Момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости (либо сила параллельна оси, либо линия действия силы пересекает ось).
16. Момент пары. Теорема о сложении пар
 Определение. Моментом пары сил называется вектор
Определение. Моментом пары сил называется вектор 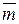 , модуль которого равен произведению модуля одной из сил пары на ее плечо и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки.
, модуль которого равен произведению модуля одной из сил пары на ее плечо и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки. 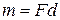 .
.
Отсюда, следует, что момент пары равен моменту одной из ее сил относительно точки приложения другой силы:
 или
или 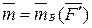
Теорема о сложении пар. Система пар, действующих на абсолютно твердое тело, эквивалентна одной паре с моментом, равным геометрической сумме моментов слагаемых пар.
Доказательство теоремы очевидно, так как по определению момент пары сил – это вектор, а векторы можно складывать:
 .
.
Из полученного результата легко найти условие равновесия системы пар, действующих на твердое тело: при равновесии должно быть 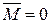 или
или 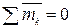 .
.
17. Теорема об эквивалентности пар, вытекающие свойства пары
Теорема. Две пары сил, имеющие одинаковые моменты, эквивалентны друг другу.
Доказательство: Рассмотрим действующую на твердое тело пару сил  и
и  . Проведем в плоскости действия этой пары через произвольные точки D и Е две параллельные прямые до пересечения их с линиями действия сил
. Проведем в плоскости действия этой пары через произвольные точки D и Е две параллельные прямые до пересечения их с линиями действия сил  ,
,  в точках А и В и приложим силы F, F' в этих точках (первоначально
в точках А и В и приложим силы F, F' в этих точках (первоначально  и
и  могли быть приложены в любых других точках на их линиях
могли быть приложены в любых других точках на их линиях  действия). Разложим теперь силу
действия). Разложим теперь силу  по направлениям АВ и ЕВ на силы
по направлениям АВ и ЕВ на силы 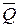 и
и 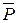 , а силу
, а силу  — по направлениям ВА и AD на силы
— по направлениям ВА и AD на силы  и
и 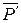 . Очевидно при этом, что
. Очевидно при этом, что 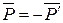 , а
, а 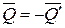 . Силы
. Силы 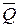 и
и  , как уравновешенные, можно отбросить. В результате пара сил
, как уравновешенные, можно отбросить. В результате пара сил  и
и  будет заменена парой
будет заменена парой 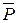 ,
, 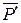 с другим плечом и другими силами, которые можно, очевидно, приложить в точках D, Е на их линиях действия. При этом в силу произвольности в выборе точек D, Е и направлений прямых AD и BE пара
с другим плечом и другими силами, которые можно, очевидно, приложить в точках D, Е на их линиях действия. При этом в силу произвольности в выборе точек D, Е и направлений прямых AD и BE пара 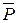 ,
, 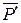 может оказаться расположенной в плоскости ее действия где угодно (в положение, при котором силы
может оказаться расположенной в плоскости ее действия где угодно (в положение, при котором силы 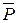 и
и 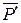 параллельны
параллельны  , пару можно привести, проделав указанное преобразование дважды).
, пару можно привести, проделав указанное преобразование дважды).
Покажем в заключение, что пары  ,
,  и
и 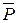 ,
, 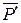 имеют одинаковые моменты. Обозначим эти моменты соответственно через
имеют одинаковые моменты. Обозначим эти моменты соответственно через 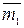 и
и  , где
, где 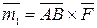 , а
, а  . Так как
. Так как 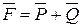 , то
, то  , но
, но 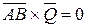 и, следовательно
и, следовательно  .
.
Из теоремы следует свойства пары сил:
1) пару, не изменяя оказываемого ею на твердое тело действия, можно переносить куда угодно в плоскости действия пары, поворачивать ее плечо на любой угол;
2) у данной пары, не изменяя оказываемого ею на твердое тело действия, можно произвольно менять модули сил или длину плеча, сохраняя неизменным ее момент.
3) пару, не изменяя оказываемого ею на твердое тело действия, можно перенести из данной плоскости в любую другую плоскость, параллельную данной.
Таким образом, вектор момента пары сил является свободным вектором.
Дата добавления: 2014-12-22; просмотров: 3941;
