Уравнения равновесия пространственной системы сил. Случай параллельных сил
Необходимыми и достаточными условиями равновесия любой системы сил являются равенства
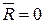 ,
, 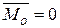


 ,
, 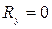 ,
,  .
.


 ,
,  ,
,  .
.
Таким образом, для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из трех координатных осей и суммы их моментов относительно этих осей были равны нулю, т.е.
1) 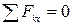 , 2)
, 2) 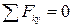 , 3)
, 3)  ;
;
4)  , 5)
, 5) 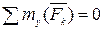 , 6)
, 6)  .
.
Если на тело кроме сил действует еще пара, заданная ее моментом 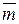 , то уравнения для сумм проекций сил не изменятся, а моментные уравнения примут вид:
, то уравнения для сумм проекций сил не изменятся, а моментные уравнения примут вид:
 ,
,  ,
,  .
.
 Случай параллельных сил. В случае, когда все действующие на тело силы параллельны друг другу, можно выбрать координатные оси так, что ось z будет параллельна силам (рис.). В этом случае
Случай параллельных сил. В случае, когда все действующие на тело силы параллельны друг другу, можно выбрать координатные оси так, что ось z будет параллельна силам (рис.). В этом случае 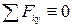 ,
, 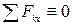 ,
, 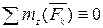 .
.
Поэтому, для равновесия пространственной системы параллельных сил необходимо и достаточно, чтобы сумма проекций всех сил на ось, параллельную силам, и суммы их моментов относительно двух других координатных осей были равны нулю.
 ,
,  ,
, 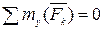 .
.
23. Центр тяжести твердого тела. Координаты центра тяжести для объёмных тел
 На каждую частицу тела, находящегося вблизи земной поверхности, действует направленная вертикально вниз сила, которую называют силой тяжести. Для тел, размеры которых очень малы по сравнению с земным радиусом, силы тяжести, действующие на частицы тела, можно считать параллельными друг другу и сохраняющими для каждой частицы постоянное значение при любых поворотах тела.
На каждую частицу тела, находящегося вблизи земной поверхности, действует направленная вертикально вниз сила, которую называют силой тяжести. Для тел, размеры которых очень малы по сравнению с земным радиусом, силы тяжести, действующие на частицы тела, можно считать параллельными друг другу и сохраняющими для каждой частицы постоянное значение при любых поворотах тела.
Равнодействующую сил тяжести  ,
,  , …,
, …,  , действующих на частицы данного тела, обозначим
, действующих на частицы данного тела, обозначим 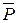 (рис.). Модуль этой силы называется весом тела и определяется равенством
(рис.). Модуль этой силы называется весом тела и определяется равенством
 .
.
Центром тяжести твердого тела называется неизменно связанная с этим телом точка, через которую проходит линия действия равнодействующей сил тяжести, действующих на частицы данного тела, при любом положении тела в пространстве.
Координаты центра тяжести определяются формулами:
 ,
, 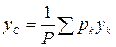 ,
, 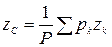 ,
,
где  ,
,  ,
,  — координаты точек приложения сил тяжести
— координаты точек приложения сил тяжести  , действующих на частицы тела.
, действующих на частицы тела.
Отметим в заключение, что согласно определению центр тяжести — это точка геометрическая, она может лежать и вне пределов данного тела (например, для кольца).
Центр тяжести объема. Для однородного тела вес  любой его части пропорционален объему
любой его части пропорционален объему  этой части:
этой части: 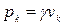 , а весь
, а весь 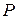 всего тела пропорционален объему
всего тела пропорционален объему  этого тела, т. е.
этого тела, т. е. 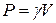 , где
, где  — вес единицы объема.
— вес единицы объема.
Подставив эти значения 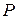 и
и  в формулы для координат цента тяжести, получим
в формулы для координат цента тяжести, получим
 ,
, 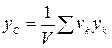 ,
, 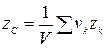 (1)
(1)
Как видно, положение центра тяжести однородного тела зависит только от его геометрической формы, а от величины  не зависит. По этой причине точку С, координаты которой определяются формулами (3), называют центром тяжести объема
не зависит. По этой причине точку С, координаты которой определяются формулами (3), называют центром тяжести объема  .
.
Дата добавления: 2014-12-22; просмотров: 2176;
