Замена переменной.
Пусть: 1) 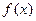 - непрерывная функция на отрезке
- непрерывная функция на отрезке  ;
;
2) функция  - дифференцируема на
- дифференцируема на  , причем
, причем 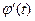 непрерывна на
непрерывна на  и множеством значений функции
и множеством значений функции  является отрезок
является отрезок  ;
;
3)  .
.
Тогда справедлива формула:  .
.
Заметим, что при подстановке следует сначала найти новые пределы интегрирования и выполнить необходимые преобразования подынтегрального выражения.
Пример 1.Вычислить интеграл 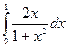 .
.
Решение: Сделаем замену:  . Тогда
. Тогда  . Пределы интегрирования: при
. Пределы интегрирования: при  и при
и при 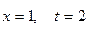 .
.
Получаем: 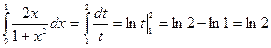 .
.
Дата добавления: 2014-12-04; просмотров: 852;
