Задачи единого государственного экзамена.

ВАРИАНТ № 1

1. Точки C, E, D делят отрезок AB в отношении 1:2, 1:3, 1:4, считая от точки A. В каком отношении точка E делит отрезок CD?

2. Биссектрисы углов равнобокой трапеции ABCD, где AD || BC, прилежащих к боковым сторонам, пересекаются в точках K и L. Найдите длину отрезка KL, если известно, что длина боковой стороны AB = 10, а длины оснований AD = 23, BC =17.

3. В прямоугольном равнобедренном треугольнике ABC, в котором угол C = 90^о, с катетами, равными 1, проведена медиана BD. На эту медиану опущен перпендикуляр CP. Найдите расстояние от точки P до точки пересечения медиан треугольника ABC.

4. В треугольнике ABC длины сторон и его площадь связаны соотношением 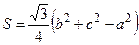. Найдите градусную меру угла A.

5. Площадь треугольника ABC равна 1,5. Найдите AC, если сторона AB равна 2 и она больше половины стороны AC, а медиана BM равна 1,25.

6. Точка K – середина стороны AD прямоугольника ABCD. Найдите угол (в градусах) между BK и диагональю AC, если известно, что .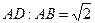

7. Внутри равностороннего треугольника взята точка, отстоящая от его сторон на расстояниях 2,4 и 5. Найдите высоту этого треугольника.

8. Точка H лежит на стороне AO треугольника AOM. Известно, что AH =4; OH =12, угол A равен 30^о, угол AMH равен углу AOM. Найдите площадь треугольника AHM.

9. Точка H лежит на стороне AO треугольника AOM. Известно, что AH = 4, OH =12, а угол A равен 30^о, угол AMH равен углу AOM. Найдите площадь треугольника AHM.

10. В параллелограмме ABCD со стороной AD = 25 проведена биссектриса угла A, проходящая через точку P на стороне BC. Найдите периметр трапеции APCD, если ее средняя линия равна 15, а диагональ AC = .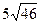

Ответы:

1. 5:3

2.

3.

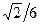
4. 60о

5. 2,5

6. 90о

7.

8.

9.

10.

ВАРИАНТ № 2

1. В треугольнике ABC угол A равен 50^о, угол B равен 70^о. Найдите острый угол, образованный биссектрисами данных углов.

2. Стороны треугольника равны 5, 6 и 7. Найдите площадь треугольника, вершинами которого служат основания биссектрис данного треугольника.

3. Найти наибольший угол в градусах треугольника со сторонами 2, 3 и .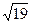

4. В треугольнике OBH точка M делит сторону OB на отрезки OM =4 и MB =28, угол OHM равен углу OBH. Найдите площадь треугольника OHM, если угол O равен 45^о.

5. Найдите расстояние от точки пересечения медиан прямоугольного треугольника до его гипотенузы, равной 25, если один из катетов равен 20.

6. Точка M лежит внутри равнобедренного треугольника ABC с основанием AC на расстоянии 6 от боковых сторон и на расстоянии 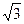от основания. Найдите основание треугольника, если угол B = 120^о.

7. Большее основание равнобедренной трапеции равно 8, боковая сторона 9, а диагональ 11. Найдите меньшее основание трапеции.

8. В треугольнике BCE медиана BM равна 3, CE = 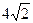, BE =5. Найдите сторону BC.

9. Стороны треугольника 12, 16 и 20. Найдите его высоту, проведенную из вершины большего угла.

10. В прямоугольный треугольник вписан квадрат, имеющий с ним общий угол. Найдите площадь квадрата, если катеты треугольника равны 10 и 15.

Ответы:

1. 60о

2.

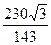
3.

4.

5.

6.

7.

8.

9. 9,6

10.

ВАРИАНТ № 3

1. Внешние углы выпуклого четырехугольника, взятые по одному при каждой вершине, относятся как 1:2:3:4. Как относятся больший и меньший углы этого четырехугольника?

2. В треугольнике ABC из вершины B к стороне AC проведен отрезок BK так, что угол ABK равен углу BCK и AK=2, CK=16. Найдите площадь треугольника ABC, если угол A = 30^о.

3. Найдите сторону AD в параллелограмме ABCD, если AB = 24, она больше AM, где M – середина AD, BM =18, а площадь четырехугольника MBCD равна .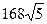

4. Найти длину медианы треугольника ABC проведенную к стороне AC, если стороны треугольника AB, BC и AC равны 2, 3 и 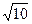соответственно.

5. Боковая сторона равнобедренной трапеции равна 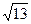, а основания равны 3 и 4. Найдите диагональ трапеции.

6. Найдите основание равнобедренного треугольника, если угол при основании равен 30^о, а взятая внутри треугольника точка находится на одинаковом расстоянии, равном 3, от боковых сторон и на расстоянии 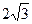от основания.

7. Диагонали трапеции KMPT с основаниями MP и KT пересекаются в точке C. Площадь треугольника MCP равна 4, KT = 2MP. Найдите площадь трапеции.

8. Найдите периметр правильного восьмиугольника ABCDEFGH, если площадь четырехугольника ABEG равна .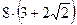

9. Основания трапеции равны 10 и 31, а боковые стороны равны 20 и 13. Найдите высоту трапеции.

10. Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите площадь параллелограмма, если BK = KC = 5, AK = 8.

Ответы:

ВАРИАНТ № 4

1. Биссектрисы внешних углов, смежных с углами B и C,пересекаются в точке D, угол A равен 40^о. Найдите угол BDC.

2. Средняя линия трапеции делится диагоналями на три равные части. Найдите отношение оснований трапеции.

3. Найдите сторону AD в параллелограмме ABCD, если AB = 12, она больше AM, где M – середина AD, BM = 9, а площадь четырехугольника MBCD равна .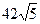

4. Две стороны треугольника равны соответственно 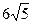и 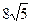. Медианы, проведенные к этим сторонам, пересекаются под прямым углом. Найти третью сторону этого треугольника.

5. Прямая, проходящая через точку пересечения диагоналей трапеции параллельно ее основаниям, пересекает боковые стороны трапеции в точках M и N. Найдите длину отрезка MN, если основания трапеции равны 7 и 3.

6. Найти длину биссектрисы угла A треугольника ABC, если угол A равен 60^о, а стороны AB и AC равны 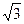и 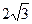соответственно.

7. В треугольнике ABC углы при стороне AB равны 30^о и 105^о. найти длину стороны, лежащей напротив угла 30^о, если длина стороны AB равна .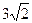

8. В треугольнике ABC проведена медиана AM, причем угол MAC = 45^о. Найдите площадь треугольника ABC, если A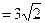C BC .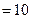

9. В треугольнике CEH угол C = 45^о, точка T делит сторону CE на отрезке CT = 2 и ET =14, угол CHT равен углу CEH. Найдите площадь треугольника CHT.

10. В прямоугольном треугольнике ABC с катетами AB и AC проведена биссектриса CD. Найдите длину стороны AC, если площадь треугольника BCD равна 24,375, а тангенс угла ADC равен 5.

Ответы: