Вписанные и описанные многоугольники.
Определение. Если все стороны многоугольника касаются окружности, то многоугольник называется описанным около окружности, а окружность – вписанной в многоугольник.
Определение. Если все вершины многоугольника лежат на окружности, то многоугольник называется вписанным в эту окружность, а окружность – описанной около треугольника.
| Вписанная окружность | Описанная окружность | |
Треугольник
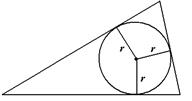 Центр – точка пересечения биссектрис.
Центр – точка пересечения биссектрис.
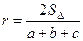 . .
| 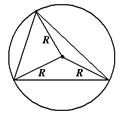 Центр – точка пересечения серединных перпендикуляров.
Центр – точка пересечения серединных перпендикуляров.
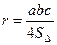 . .
| |
| Параллелограмм НЕТ | НЕТ | |
Ромб
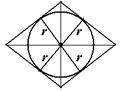 Центр – точка пересечения диагоналей.
Радиус окружности равен половине высоты ромба, т.е.
Центр – точка пересечения диагоналей.
Радиус окружности равен половине высоты ромба, т.е. 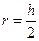 . .
| НЕТ | |
| Прямоугольник НЕТ | 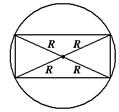 Центр – точка пересечения диагоналей.
Радиус окружности равен половине длины диагонали прямоугольника, т.е.
Центр – точка пересечения диагоналей.
Радиус окружности равен половине длины диагонали прямоугольника, т.е. 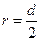 . .
| |
Квадрат
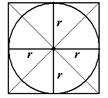 Центр – точка пересечения диагоналей.
Радиус окружности равен половине длины стороны квадрата, т.е.
Центр – точка пересечения диагоналей.
Радиус окружности равен половине длины стороны квадрата, т.е. 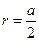 . .
| 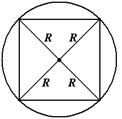 Центр – точка пересечения диагоналей.
Радиус окружности равен половине длины диагонали квадрата, т.е.
Центр – точка пересечения диагоналей.
Радиус окружности равен половине длины диагонали квадрата, т.е. 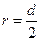 . .
| |
Трапеция
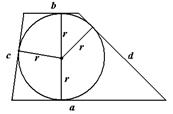 Центр – точка пересечения биссектрис.
В трапецию можно вписать окружность тогда и только тогда, когда суммы длин противоположных сторон равны, т.е.
Центр – точка пересечения биссектрис.
В трапецию можно вписать окружность тогда и только тогда, когда суммы длин противоположных сторон равны, т.е.
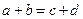 .
Радиус окружности равен половине длины высоты трапеции, т.е. .
Радиус окружности равен половине длины высоты трапеции, т.е. 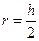 . .
| 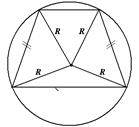 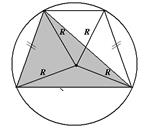 Центр – точка пересечения серединных перпендикуляров.
Около трапеции можно описать окружность тогда и только тогда, когда трапеция равнобедренная.
Радиус окружности можно найти как радиус описанной окружности около треугольника, вершинами которого являются вершины трапеции (любые три из четырех у трапеции).
Центр – точка пересечения серединных перпендикуляров.
Около трапеции можно описать окружность тогда и только тогда, когда трапеция равнобедренная.
Радиус окружности можно найти как радиус описанной окружности около треугольника, вершинами которого являются вершины трапеции (любые три из четырех у трапеции).
| |
Произвольный выпуклый четырехугольник
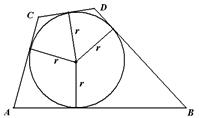 Центр – точка пересечения биссектрис.
В произвольный выпуклый четырехуголь-ник можно вписать окружность тогда и только тогда, когда суммы длин противоположных сторон равны, т.е.
Центр – точка пересечения биссектрис.
В произвольный выпуклый четырехуголь-ник можно вписать окружность тогда и только тогда, когда суммы длин противоположных сторон равны, т.е.
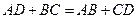 .
Общего способа и формулы для вычисления длины радиуса нет.
. .
Общего способа и формулы для вычисления длины радиуса нет.
.
|
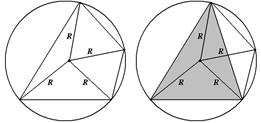 Центр – точка пересечения серединных перпендикуляров.
Около произвольного выпуклого четырехугольника можно описать окружность тогда и только тогда, когда суммы противоположных углов равны
Центр – точка пересечения серединных перпендикуляров.
Около произвольного выпуклого четырехугольника можно описать окружность тогда и только тогда, когда суммы противоположных углов равны 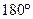 .
Радиус окружности можно найти как радиус описанной окружности около треугольника, вершинами которого являются вершины данного четырехугольника (любые три из его четырех).
Теорема 39. (Птолемея). В четырехуголь-нике, вписанном в окружность, произведение диагоналей равно сумме произведений противоположных сторон. .
Радиус окружности можно найти как радиус описанной окружности около треугольника, вершинами которого являются вершины данного четырехугольника (любые три из его четырех).
Теорема 39. (Птолемея). В четырехуголь-нике, вписанном в окружность, произведение диагоналей равно сумме произведений противоположных сторон.
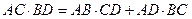
| |
Определение. Выпуклый многоугольник называется правильным, если у него все углы равны и стороны равны.
Теорема 38. Около любого правильного многоугольника можно описать окружность и притом только одну.
Теорема 39. В любой правильный многоугольник можно вписать окружность и притом только одну.

| Площадь S правильного n-угольника, сторона an, периметр P и радиусы r вписанной окружности и R описанной окружности связаны соотношениями:
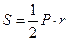 ; ;
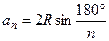 ; ;
 . .
|
Дата добавления: 2014-12-22; просмотров: 4297;
