Площади плоских фигур.

Определение. Пусть каждой плоской фигуре соответствует единственное положительное действительное число так, что выполняются условия:

1) Равным фигурам соответствует одно и тоже число.

2) Если некоторая линия разлагает фигуру на две и каждой образованной фигуре соответствуют определенные числа, то всей фигуре соответствует число, равное сумме чисел, соответствующих ее частям.

3) Квадрату, построенному на выбранном единичном отрезке, соответствует число, равное единице.

Число, указанным образом соответствующее данной фигуре, называется площадью фигуры.

Приведем без доказательств формулы вычисления плоских фигур.

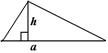
	Площадь треугольника равна половине произведения длины основания треугольника на длину высоту, проведенной к основанию. .
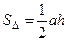	Площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.
	Формула Герона , где р – полупериметр.
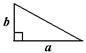
	Площадь прямоугольного треугольника равна половине произведения длин его катетов.
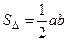
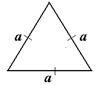
	Площадь равностороннего треугольника можно вычислить по формуле 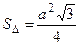, где а – длина сторон правильного треугольника.
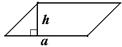
	Площадь параллелограмма равна произведению длины основания на длину высоты, проведенной к основанию.
	Площадь параллелограмма равна произведению длин двух смежных сторон параллелограмма на синус угла между ними.
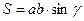
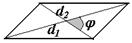
	Площадь параллелограмма равна половине произведения длин диагоналей параллелограмма на синус угла между ними. .
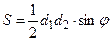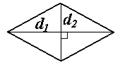
	Площадь ромба равна половине произведения длин его диагоналей. .
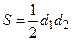	Площадь прямоугольника равна произведению длин его смежных сторон .
	Площадь квадрата равна квадрату длины его стороны .
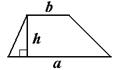
	Площадь трапеции равна произведению полусуммы длин оснований на длину высоты. .
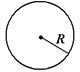
	Площадь круга можно вычислить по формуле: .
	Площадь сектора
	Площадь сегмента

Примечание. Формула вычисления площади правильного многоугольника будет дана в следующем пункте лекции.