Окружность и круг.
Определение. Окружностью называется фигура, состоящая из множества всех точек плоскости, каждая из которых находится на данном расстоянии r от некоторой точки О этой плоскости. Точка О называется центром окружности, а отрезок, соединяющий точку О с любой точкой окружности, – ее радиусом. Все радиусы окружности имеют длину r. Число r также называется радиусом окружности.
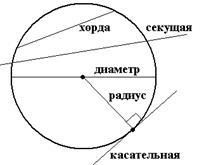
| Определение. Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром окружности. Определение. Прямая, пересекающая окружность в двух точках, называется секущей. Определение. Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности. |
Две произвольные точки А и В окружности разбивают все точки окружности, отличные от А и В, на два множества.
Определение. Фигура, состоящая из объединения каждого из этих множеств с точками А и В называются дугой окружности, а точки А и В – концами двух этих дуг.
Определение. Дуга называется полуокружностью, если отрезок, соединяющий ее концы, является диаметром.
Определение. Угол, вершина которого совпадает с центром О окружности, называется ее центральным углом.
Введем понятие градусной меры дуги.
Если дуга АВ окружности с центром О не больше полуокружности, то градусной мерой этой дуги считают градусную меру центрального угла АОВ. Если же дуга АВ больше полуокружности, то ее градусная мера считается равной 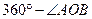 . Отсюда следует, что градусная мера полуокружности равна . Отсюда следует, что градусная мера полуокружности равна 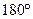 , а сумма градусных мер двух дуг окружности с общими концами А и В равна , а сумма градусных мер двух дуг окружности с общими концами А и В равна 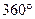 .
Свойства градусных мер дуг окружностей. .
Свойства градусных мер дуг окружностей.
| |
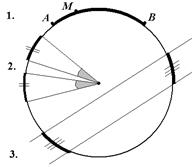
| 1. Если точка М лежит на дуге АВ, то градусная мера дуги АВ равна сумме градусных мер дуг АМ и МВ. 2. Две дуги одной окружности или двух окружностей с равными радиусами равны тогда и только тогда, когда они имеют равные градусные меры. 3. Две дуги окружности, заключенные между параллельными секущими, равны. |
Определение. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
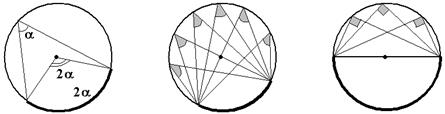
Теорема 37. Вписанный угол измеряется половиной дуги, на которую он опирается.
Следствие. Вписанные в окружность углы, опирающиеся на одну и ту же дугу, равны. В частности, вписанные в окружность углы, опирающиеся на полуокружность, прямые.
Углы между касательными, хордами и секущими.
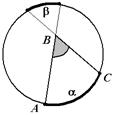
| 1. Градусная мера угла, вершина которого расположена внутри окружности, равна полусумме градусных мер дуг, одна из которых та, на которую опирается данный угол, а другая – на которую опираются продолжения лучей данного угла.
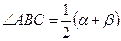 . .
| ||||
| 2. Градусная мера угла, вершина которого расположена вне окружности, равна полуразности градусных мер дуг, на которые опирается данный угол, причем из большей меры надо вычесть меньшую. | |||||
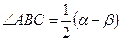 . .
| Это утверждение верно, если | ||||
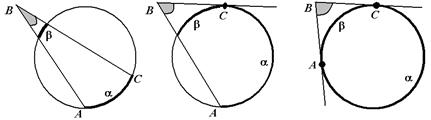
| – оба луча – секущие; – один луч – секущий, а второй направлен по касательной; – оба луча направлены по касательным. | ||||
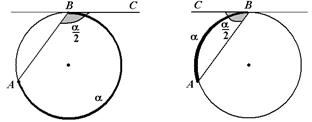
| 3. Градусная мера угла, одна из сторон которого направлена по хорде, а другая по касательной к окружности, равна половине градусной меры дуги окружности, заключенной внутри угла.
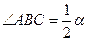 . .
| ||||
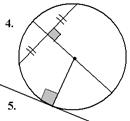
| 4. Диаметр окружности перпендикулярен к хорде, не проходящей через центр окружности, тогда и только тогда, когда он проходит через середину хорды. 5. Прямая является касательной к окружности тогда и только тогда, когда она проходит через точку окружности перпендикулярно к радиусу, проведенного в эту точку. | ||||
Соотношения между хордами, радиусами и отрезками секущих и касательных.
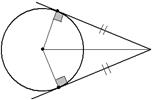
| 1. Если из точки, лежащей вне окружности, проведены две касательные к данной окружности, то длины отрезков, заключенных между данной точкой и точками касания, равны. |
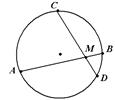
| 2. Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
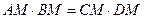 . .
|
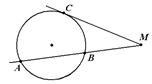
| 3. Если из точки вне окружности проведены секущая и касательная, то произведение отрезков, заключенных между данной точкой и точками пересечения секущей с окружностью равно квадрату отрезка, заключенного между данной точкой и точкой касания окружности касательной.
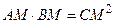 . .
|
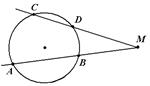
| 4. Если из точки вне окружности проведены две секущие, то произведение длин отрезков, заключенных между данной точкой и точками пересечения с окружностью одной секущей равно произведение длин отрезков, заключенных между данной точкой и точками пересечения с окружностью другой секущей.
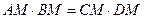
|
Длину окружности можно вычислить по формуле: 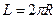 .
.
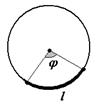
| Длину дуги окружности, имеющую угловую меру 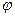 , можно вычислить по формуле: , можно вычислить по формуле:
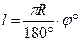 , если угол , если угол 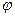 измеряется в градусах; измеряется в градусах;
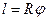 , если угол , если угол 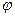 измеряется в радианах. измеряется в радианах.
|
Дата добавления: 2014-12-22; просмотров: 1922;
