Метрические соотношения в треугольнике.
Соотношения между сторонами и углами треугольника.
| 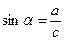
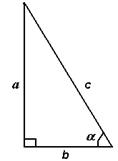
| В прямоугольном треугольнике синус угла равен отношению противолежащего катета к гипотенузе. |
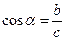
| В прямоугольном треугольнике косинус угла равен отношению прилежащего катета к гипотенузе. | |
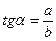
| В прямоугольном треугольнике тангенс угла равен отношению противолежащего катета к прилежащему. | |
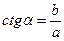
| В прямоугольном треугольнике котангенс угла равен отношению прилежащего катета к противолежащему. |
Теорема 24. (Пифагора) В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Теорема 25. (Теорема, обратная теореме Пифагора) Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
С помощью теоремы, обратной к теореме Пифагора, можно по длинам сторон определить, является он прямоугольным или нет.
Наиболее интересны прямоугольные треугольники с целочисленными длинами сторон. Так, например, треугольники
3, 4, 5 и далее им подобные 6, 8, 10, далее 9, 12, 15 и т.д.
5, 12, 13 и далее им подобные 10, 24, 26 и т.д.
8, 15, 17 и далее им подобные.
7, 24, 25 и далее им подобные.
Скорее всего таких независимых серий прямоугольных треугольников с целочисленными длинами сторон бесконечно много.
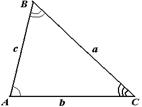
| Теорема 26. (синусов)
Стороны треугольника пропорциональны синусам противолежащих углов.
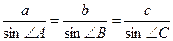 .
Следствием к теореме синусов можно считать следующую теорему.
Теорема 27.
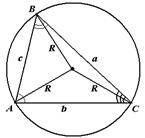
Стороны треугольника пропорциональны синусам противолежащих углов и их отношения равны двум радиусам описанной окружности около данного треугольника.. .
Следствием к теореме синусов можно считать следующую теорему.
Теорема 27.
Стороны треугольника пропорциональны синусам противолежащих углов и их отношения равны двум радиусам описанной окружности около данного треугольника..
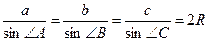 . .
|

| Теорема 28. (косинусов)
Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
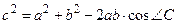 . .
|
Дата добавления: 2014-12-22; просмотров: 7999;
