Признаки подобия треугольников.
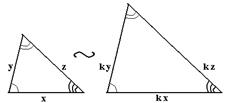
| Определение. Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого. |
То есть если 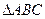 ~
~ 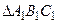 , то
, то 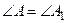 ,
, 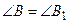 ,
, 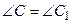 и
и 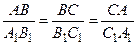 .
.
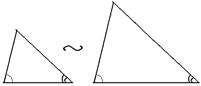
| Теорема 18. (Первый признак подобия треугольников) Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны. |
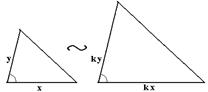
| Теорема 19. (Второй признак подобия треугольников) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны. |
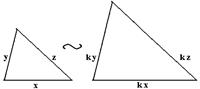
| Теорема 20. (Третий признак подобия треугольников) Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. |
С помощью признаков подобия легко доказать теорему Фалеса.
Теорема 21. (Фалеса) Параллельные прямые, пересекающие две данные прямые и отсекающие на одной из них равные отрезки, отсекает на другой прямой равные отрезки.
С помощью признаков подобия легко доказать следующую теорему.
Теорема 22. Высота, проведенная из вершины прямого угла прямоугольного треугольника, делит его на два треугольника, подобных данному и подобных между собой.
Из этой теоремы можно получить некоторые метрические соотношения для прямоугольного треугольника.
Теорема 23. В прямоугольном треугольнике:
а) высота, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые гипотенуза делится высотой;
б) катет есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой, проведенной из вершины прямого угла.
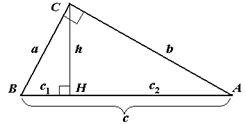
| Из подобия треугольников
 ~ ~ 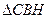 , ,
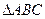 ~ ~ 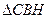 , ,
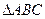 ~ ~ 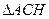 Следуют соотношения
Следуют соотношения 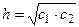 , ,
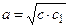 , ,
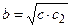 . .
|
Дата добавления: 2014-12-22; просмотров: 1556;
