Классификация треугольников.

Классифицировать треугольники можно по длинам сторон и по величинам углов.

По величинам углов треугольники подразделяются на остроугольные; прямоугольные; тупоугольные.

Определение. Если все углы треугольника острые, то треугольник называется остроугольным; если один угол треугольника прямой, то треугольник называется прямоугольным; если один угол треугольника тупой – тупоугольным. В прямоугольном треугольнике сторона, лежащая против прямого угла, называется гипотенузой, а две другие стороны – катетами.

По длинам сторон треугольники подразделяются на разносторонние (произвольные), равнобедренные и равносторонние.

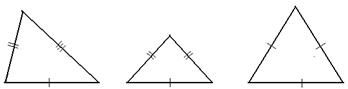
Определение. Если стороны треугольника попарно не равны, то треугольник называется разносторонним. Треугольник называется равнобедренным, если две его стороны равны. Треугольник, все стороны которого равны, называется равносторонним.

В равнобедренном треугольнике равные стороны называются боковыми сторонами, а третья сторона – основанием равнобедренного треугольника.

Теорема 8. (Свойства равнобедренного треугольника).

В равнобедренном треугольнике:

а) углы при основании равны (и острые);

б) медиана, биссектриса, высота и серединный перпендикуляр, проведенные к основанию, совпадают.

в) медианы, проведенные к боковым сторонам, равны.

г) биссектрисы, проведенные к боковым сторонам, равны.

д) высоты, проведенные к боковым сторонам, равны.

Теорема 9. (Признаки равнобедренного треугольника).

а) Если в треугольнике два угла равны, то треугольник равнобедренный (сторона, к которой прилежат оба равных угла – основание).

б) Если в треугольнике совпадают любые две из четырех линий (медиана, биссектриса, высота, серединный перпендикуляр), проведенные к некоторой стороне треугольника, то треугольник равнобедренный (а эта сторона является основанием).

в) Если в треугольнике две медианы равны, то треугольник равнобедренный (а стороны, к которым проведены медианы – боковые).

г) Если в треугольнике две биссектрисы равны, то треугольник равнобедренный (а стороны, к которым проведены биссектрисы – боковые).

д) Если в треугольнике две высоты равны, то треугольник равнобедренный (а стороны, к которым проведены высоты – боковые).

Теоремы, связывающие углы треугольника.

Теорема 10. Сумма углов треугольника равна 180^о.

Из этой теоремы непосредственно следует, что в треугольнике не может быть более одного прямого и более одного тупого угла.

Определение. Угол, смежный с углом треугольника, называется внешним углом треугольника.

Теорема 11. Внешний угол треугольника равен сумме двух внутренних, не смежных с ним.

Теорема, связывающая стороны треугольников.

Теорема 12. Сумма длин двух сторон треугольника больше длины третьей стороны.

Теорема, связывающая стороны и углы треугольников.

Теорема 13. Против большего угла треугольника лежит большая сторона. Против большей стороны треугольника лежит больший угол.