Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.

Углы.

Определение. Углом называется геометрическая фигура, состоящая из точки и двух лучей, исходящих из этой точки. Точка называется вершиной угла, а лучи – его сторонами.

Определение. Угол называется развернутым, если его стороны являются дополнительными лучами.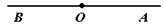
С каждым неразвернутым углом АОВ связаны две полуплоскости: полуплоскость с границей ОА, которой принадлежит сторона ОВ и полуплоскость с границей ОВ, которой принадлежит сторона ОА. Определение. Пересечение этих полуплоскостей называется внутренней областью данного угла.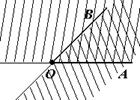

Определение. Точки, принадлежащие внутренней области угла, называют внутренними относительно угла или точками, лежащими внутри угла. Точки плоскости, не принадлежащие внутренней области угла и не являющиеся точками угла, называются внешними относительно угла.

Определение. Луч, который исходит из вершины неразвернутого угла и целиком состоит из внутренних точек относительно угла, называется внутренним лучом угла.

Теорема 1. Любой внутренний луч неразвернутого, угла делит этот угол на два угла.

Определение. Два неразвернутых угла называются смежными, если одна сторона у них общая, а две другие стороны являются дополнительными лучами. Два неразвернутых угла называются вертикальными, если стороны одного угла являются соответственно дополнительными лучами сторон другого угла.

Теорема 2. Если неразвернутые углы равны, то углы соответственно смежные с ними также равны.

Теорема 3. Вертикальные углы равны.

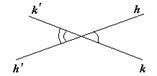
Каждый неразвернутый угол имеет два смежных с ним угла.

Теорема 4. Сумма смежных углов равна 180^о.

Определение. Угол называется прямым,если он равен каждому из углов, смежных с ним.

Очевидно, что прямой угол имеет градусную меру, равную 90^о.

Две пересекающиеся прямые образуют четыре неразвернутых угла. Если один из этих углов прямой, то, очевидно, что остальные три угла также прямые. В этом случае говорят, что данные прямые взаимно перпендикулярны.

Определение. Две пересекающиеся прямые называются перпендикулярными(или взаимно перпендикулярными), если они при пересечении образуют четыре прямых угла.

Перпендикулярность прямых а и b обозначается так: .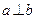

Теорема 5. Через каждую точку плоскости проходит прямая, перпендикулярная к данной прямой, и притом только одна.

Следствие. Две прямые, перпендикулярные к одной прямой, не пересекаются.

Определение. Угол, меньший прямого угла, называется острым. Неразвернутый угол, больший прямого угла, называется тупым.

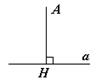
Рассмотрим прямую а и точку А, не лежащую на ней. Отрезок, соединяющий точку А с точкой H прямой а, называется перпендикуляром,проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. В этом случае точка H называется основанием перпендикуляра.

Из теоремы о перпендикулярных прямых непосредственно следует утверждение:

Следствие. Из точки, не лежащий на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

Пусть прямая MN – секущая по отношению к прямым АВ и СD. Тогда образуется 8 углов, имеющих свои названия.

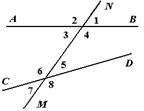
Углы 1и 5, 2 и 6, 3 и 7, 4 и 8 называются соответственными. Углы 3 и 5, 4 и 6 называются внутренними накрест лежащими. Углы 3 и 6, 4 и 5 называются внутренними односторонними.

Теорема 6. (признаки параллельности прямых) Две прямые параллельны, если при пересечении их секущей выполняется хотя бы одно из условий:

а) накрест лежащие углы равны;

б) соответственные углы равны;

в) сумма внутренних односторонних углов равна 180^о.

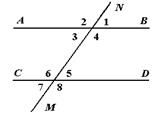
Верна и обратная теорема.

Теорема 7. (свойства параллельных прямых) Если две параллельные прямые пересечены секущей, то:

а) накрест лежащие углы равны;

б) соответственные углы равны;

в) сумма внутренних односторонних углов равна 180^о.