Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
Источник:Фокус
Share1 4
Основные понятия.
Аксиомы планиметрии.
Углы.
Треугольники.
Замечательные линии и точки треугольника.
Классификация треугольников.
Признаки равенства треугольников.
Признаки подобия треугольников.
Метрические соотношения в треугольнике.
Многоугольники.
Окружность и круг.
Площади плоских фигур.
Вписанные и описанные многоугольники.
Задачи для самостоятельного решения.
Задачи централизованного тестирования.
Задачи единого государственного экзамена.
Основные понятия.
Некоторые простейшие геометрические понятия, знакомые нам по опыту, принимаются за основные понятия. При изучении геометрии на плоскости основными считаются понятия точки, прямой (основные объекты), а также понятия «точка лежит на прямой», «точка лежит между двумя точками», «наложение» (основные отношения). Определения основных понятий не даются. Всем другим понятиям будем давать точное определение, исходя из основных понятий и ранее введенных понятий. К таким можно отнести понятия отрезка, луча, полуплоскости, угла, треугольника, многоугольника и другие.
Свойства основных понятий выражаются в предложениях, которые называются аксиомами. Аксиомы – это те основные положения геометрии, которые принимаются без доказательства в качестве исходных. Все остальные предложения геометрии мы должны вывести из аксиом или ранее полученных утверждений с помощью строгих логических рассуждений, т.е. с помощью доказательств. (Очевидно, что в нашей обзорной лекции доказательства приводиться не будут.)
Аксиомы планиметрии.
Сформулируем первые три аксиомы планиметрии, которые называются аксиомами принадлежности. Они характеризуют взаимное расположение точек и прямых.
I1. На каждой прямой лежат по крайней мере две точки.
I2. Существуют по крайней мере три точки, не лежащие на одной прямой.
I3. Через любые две точки проходит прямая, и притом только одна.
(Здесь и в дальнейшем, говоря «две точки», «три прямые», будем считать, что рассматриваемые точки, прямые различны.)
Следующая группа аксиом – аксиомы порядка.
II1. Если точка В лежит между точкой А и точкой С, то А, В, С – три различные точки некоторой прямой и точка В лежит также между точкой С и точкой А.
II2. Из трех точек прямой одна и только одна лежит между двумя другими.
II3. Каждая точка О, лежащая на прямой, разделяет множество остальных точек этой прямой на два непустых подмножества так, что точка О лежит между любыми двумя точками различных подмножеств и не лежит между любыми двумя точками одного и того же подмножества.
II4. Каждая прямая а разделяет множество всех точек плоскости, не лежащих на этой прямой, на два подмножества так, что любые две точки разных подмножеств лежат по разные стороны от прямой a, а любые две точки одного и того же подмножества лежат по одну сторону от прямой а.
В аксиомах группы III выражены свойства наложений, состоящей из семи аксиом.
Определение. Фигуры называются равными, если они совпадают при наложении.
III1. Каждая фигура равна самой себе.
III2. Если фигура Ф равна фигуре Ф', то фигура Ф' равна фигуре Ф.
III3. Если фигура Ф1 равна фигуре Ф2, а фигура Ф2 равна фигуре Ф3, то фигура Ф1 равна фигуре Ф3.
III4. Если при наложении концы отрезка АВ отображаются в концы отрезка А'В', то отрезок АВ отображается на отрезок А'В'.
Рассмотрим некоторые свойства наложений, которые вытекают из сформулированных аксиом.
1). При наложении различные точки переходят в различные точки.
2). При наложении три точки, не лежащие на одной прямой, переходят в три точки, также не лежащие на одной прямой.
III5. На любом луче от его начала можно отложить отрезок, равный данному, и притом только один.
Пользуясь этой аксиомой, можно доказать следующее важные свойства наложений.
3). Если при наложении две точки А и В переходят соответственно в точки А' и В', то луч АВ переходит в луч А'В'.
4). При наложении прямая отображается на прямую.
5). Если при наложении луч ОА переходит в себя, то каждая точка прямой ОА переходит в себя.
6). При наложении неразвернутый угол переходит в неразвернутый угол, и внутренний луч неразвернутого угла переходит во внутренний луч неразвернутого угла.
III6. Если hk – неразвернутый угол и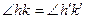 
, то существует наложение, при котором луч h переходит в луч h', а луч k – в луч k'.
Из аксиомы III6 следует, что если 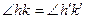, то существуют два наложения: при одном из них луч h переходит в луч h', а луч k – в луч k', а при другом – луч h переходит в луч k', а луч k – в луч h'.
III7. От любого луча в данную полуплоскость можно отложить угол, равный данному неразвернутому углу, и притом только один.
Введем важное понятие геометрии – длину отрезка.
Определение. Пусть каждому отрезку соответствует определенное положительное число так, что:
Д1. Равным отрезкам соответствует одно и то же число.
Д2. Если В – точка, лежащая на отрезке АС, и отрезкам АВ и ВС соответствуют числа а и b , то отрезку АС соответствует число а + b.
Д3. Некоторому произвольно выбранному отрезку PQ соответствует число, равное единице.
Тогда число, указанным образом соответствующее каждому отрезку, называется длинойэтого отрезка. Отрезок PQ называется единицей измерения или единичным отрезком.
Аксиома существования длины отрезка.
IV1. При произвольно выбранном единичном отрезке каждый отрезок имеет определенную длину.
Другими словами, аксиома утверждает, что измерение отрезков возможно, т.е. при произвольно выбранном единичном отрезке каждому отрезку соответствует определенное число, которое удовлетворяет условиям Д1, Д2 и Д3.
Аксиома существования отрезка данной длины.
IV2. Для любого вещественного положительного числа а существует отрезок, длина которого, при выбранном единичном отрезке, равна а.
Определение. Две прямые на плоскости, не имеющие ни одной общей точки, называются параллельными.
Аксиома параллельных прямых.
V. Через точку, не лежащую на данной прямой, проходит не более одной прямой, параллельной данной.
Геометрия, построенная на аксиомах групп I – IV, называется абсолютной геометрией. В абсолютной геометрии имеют место теоремы, при доказательстве которых не используется аксиома параллельных прямых.
Постулат Евклида.
Евклид – древнегреческий математик, жил примерно от 330 до 275 г. до н.э. в Египте. Он автор первого из дошедших до нас теоретических трактатов по математике. Его основная работа «Начала» содержит систематическое изложение планиметрии и стереометрии. В «Началах» содержится также изложение ряда вопросов теории чисел.
«Начала» Евклида состоят из 13 книг. Каждая книга начинается с определения всех тех понятий, которые в ней встречаются. Затем приводятся предложения, принимаемые без доказательств – постулаты и аксиомы. На основе этого Евклид излагает теоремы геометрии, располагая их в такой последовательности, чтобы каждую теорему можно было доказать, используя только предыдущие предложения, постулаты и аксиомы.
Некоторые из аксиом и постулатов Евклида и сейчас используются в курсе геометрии в современной формулировке. Сама геометрия, изложенная в «Началах», называется евклидовой геометрией.
Среди постулатов и аксиом пятый постулат Евклида играет существенную роль, так как на нем основана теория параллельных прямых и все связанные с ней разделы.
Этот постулат формулируется так: Если прямая при пересечении с двумя другими прямыми образует с ними односторонние углы, сумма которых меньше двух прямых, то эти прямые пересекаются с той стороны, с которой эта сумма меньше двух прямых.
Можно доказать, что пятый постулат Евклида эквивалентен аксиоме параллельных прямых.
Существует много других предложений, эквивалентных аксиоме параллельных прямых или пятому постулату Евклида. Сформулируем некоторые из них.
а) Сумма углов любого треугольника равна 180о.
б) Существует по крайней мере один треугольник, сумма углов которого равна 180°.
в) Если отрезки АС и BD равны и перпендикулярны к прямой АВ, а точки С и D лежат по одну сторону от прямой АВ, то CD = АВ.
г) Множество всех точек плоскости, лежащих по одну сторону от данной прямой и равноудаленных от этой прямой, есть прямая, параллельная данной.
д) Если три точки, лежащие по одну сторону от данной прямой, равноудалены от этой прямой, то эти точки лежат на прямой.
е) Если две прямые не перпендикулярны, то любая прямая, перпендикулярная к одной из них, пересекает другую прямую.
Многие математики, начиная с древних времен и до конца первой четверти XIX столетия, делали неоднократные попытки доказать пятый постулат Евклида (или предложения, ему равносильные). Все эти попытки оказались, однако, неудачными.
И только в начале XIX века были получены результаты, которые привели к решению этой проблемы. Основная заслуга в этом принадлежит знаменитому русскому ученому Н.И. Лобачевскому.
Николай Иванович Лобачевский родился 2 декабря 1792 г. в Нижнем Новгороде. Он окончил гимназию при Казанском университете, а затем и Казанский университет, после чего был оставлен там преподавателем. С 1816 г. Н.И. Лобачевский – профессор того же университета, с 1827 по 1846 г. – ректор университета. Н.И. Лобачевский скончался 24 февраля 1856 г.
В течение первых лет преподавательской деятельности в Казанском университете Н.И. Лобачевский настойчиво пытался доказать V постулат. Неудачи этих попыток и попыток его предшественников привели его к выводу, что V постулат не может быть выведен из остальных постулатов геометрии. Чтобы это доказать, Н.И. Лобачевский построил логическую систему, в которой, сохраняя основные посылки Евклида, онотверг V постулат Евклида и заменил его противоположным допущением. Он пришел к выводу, что эта логическая схема представляет собой новую геометрию, которая может быть развита так же успешно, как и геометрия Евклида.
7 февраля 1826 г. Н.И. Лобачевский представил физико-математическому факультету Казанского университета доклад по теории параллельных под названием «Рассуждения о принципах геометрии». В 1829г. в Ученых записках Казанского университета поместил статью «О началах геометрии».
Лобачевский развивает свою геометрию на плоскости и в пространстве до тех же пределов, до каких была развита евклидова геометрия, включая и формулы тригонометрии. Эту геометрию он назвал «воображаемой» (впоследствии ее стали называть геометрией Лобачевского или гиперболической геометрией).
Позднее, в конце XIX века, благодаря работам Ф. Клейна, Б. Римана и других математиков, проблема пятого постулата была решена полностью: пятый постулат Евклида не зависит от остальных аксиом абсолютной геометрии.
Примерно в одно время с Лобачевским теорией параллельных прямых занимались великий немецкий математик К.Ф. Гаусс (1777–1855) и венгерский математик Я. Бояи (1802–1860). Но Гаусс не опубликовал ничего по теории параллельных, боясь, что его не поймут. После смерти Гаусса в его бумагах были найдены наброски отдельных наиболее простых теорем гиперболической геометрии. Я. Бояи опубликовал в 1832 г. (через три года после публикации Лобачевского и не зная о последней) на латинском языке произведение «Приложение, излагающее абсолютно верное учение о пространстве, независимое от правильности или ложности XI аксиомы Евклида...», В этой работе Янош Бояи изложил ту же теорию, что и Лобачевский, но в значительно менее развитой форме.
Аксиомы планиметрии в школе.
Основными свойствами принадлежности точек и прямых на плоскости мы будем называть следующие свойства:
Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
Через любые две точки можно провести прямую, и только одну.
Основным свойством расположения точек на прямой мы будем называть следующее свойство:
Дата добавления: 2014-12-22; просмотров: 7100;