Признаки равенства треугольников.
Определение. Две фигуры называются равными, если они совпадают при наложении.
Определение. Два треугольника называются равными, если соответственные их стороны и углы равны.
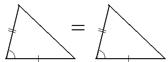
| Теорема 14. (Первый признак равенства треугольников) Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. |
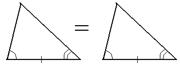
| Теорема 15. (Второй признак равенства треугольников) Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. |
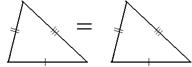
| Теорема 16. (Третий признак равенства треугольников) Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. |
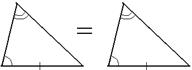
| Еще один признак равенства треугольников, который не изучается в школьном курсе геометрии. Теорема 17. Если два угла одного треугольника соответственно равны двум углам другого и сторона первого треугольника, противолежащая одному из этих углов, равна соответствующей стороне второго треугольника, то такие треугольники равны. |
Рассмотренные четыре признака равенства треугольников могут быть применены и к прямоугольным треугольникам. В этом случае соответствующие признаки несколько упрощаются, так как угол, образованный катетами прямоугольного треугольника – прямой, а любые два прямых угла равны.
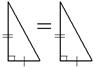
| 1°. Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то треугольники равны. |
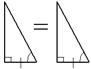
| 2°. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то треугольники равны. |
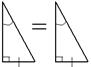
| 3°. Если катет и противолежащий угол одного прямоугольного треугольника соответственно равны катету и противолежащему углу другого, то треугольники равны. |
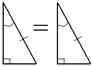
| 4°. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то треугольники равны. |
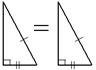
| 5°. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны. |
Признаки равенства треугольников, в частности прямоугольных треугольников, рассмотренные выше, основаны на равенстве основных элементов – сторон и углов треугольника. Однако можно сформулировать и другие признаки равенства треугольников, основанные на равенстве других элементов треугольников, отличных от сторон и углов. В следующей задаче сформулировано несколько таких признаков, доказательство которых нетрудно выполнить самостоятельно.
Задача. Даны треугольники ABC и 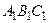 , CH и
, CH и 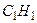 –высоты этих треугольников, СМ и
–высоты этих треугольников, СМ и 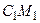 – их медианы. Доказать, что в каждом из следующих случаев треугольники ABC и
– их медианы. Доказать, что в каждом из следующих случаев треугольники ABC и 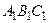 , равны:
, равны:
а) 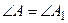 ,
, 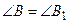 , СН =
, СН = 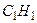 ;
;
б) АВ = 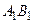 , СМ =
, СМ = 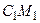 , СН =
, СН = 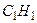 ;
;
в) СА = 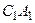 , СВ =
, СВ = 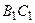 , СМ =
, СМ = 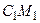 ;
;
г) СМ = 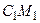 ,
, 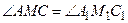 ,
, 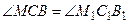 .
.
Дата добавления: 2014-12-22; просмотров: 1732;
