Замечательные линии и точки треугольника.

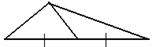
Определение. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

Медианы треугольника обладают следующими свойствами.

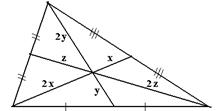
	1. Все точки, лежащие на медиане треугольника, принадлежат внутренней области треугольника. 2. Каждый треугольник имеет три медианы. 3. Три медианы треугольника пересекаются в одной точке (центр тяжести треугольника). 4. Точкой пересечения медианы делятся в отношении 2:1 считая от вершины.
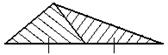
	5. Медиана треугольника делит его на два равновеликих (равных по площади) треугольника.

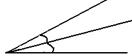
	Определение. Биссектрисой угла называется луч, делящий угол на два равных угла.
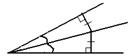
	Свойство биссектрисы угла. Любая точка с биссектрисы угла равноудалена от ее сторон.
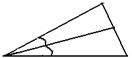
	Определение. Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.

Биссектрисы треугольника обладают следующими свойствами.

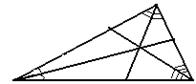
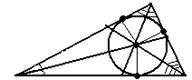
	1. Все точки, лежащие на биссектрисе треугольника, принадлежат внутренней области треугольника.   2. Каждый треугольник имеет три биссектрисы.   3. Три биссектрисы треугольника пересекаются в одной точке.   4. Точка пересечения биссектрис – центр вписанной окружности.
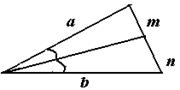
	5. Биссектриса угла треугольника делит его противоположную сторону на отрезки, пропорциональные боковым сторонам. Т.е. .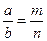

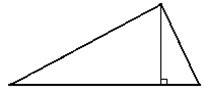
Определение. Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.

Высоты треугольника обладают следующими свойствами.

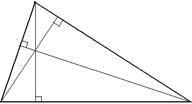
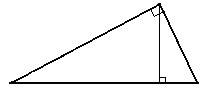
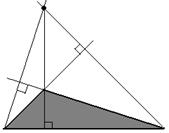
1. Каждый треугольник имеет три высоты. 2. Все точки, лежащие на высоте остроугольного треугольника, принадлежат внутренней области треугольника. В прямоугольном треугольнике две высоты совпадают с его катетами, а точки, лежащие на высоте, проведенной из вершины прямого угла, принадлежат внутренней области треугольника. В тупоугольном треугольнике точки, лежащие на высоте, проведенной из вершины тупого угла, принадлежат внутренней области треугольника, а на двух других высотах нет ни одной точки внутренней области треугольника. 3. Высоты остроугольного треугольника пересекаются в одной точке; высоты прямоугольного треугольника пересекаются в вершине прямого угла; в тупоугольном треугольнике высоты не имеют общих точек, но прямые, содержащие эти высоты, пересекаются в одной точке. В любом из этих случаев точка пересечения высот называется ортоцентром.

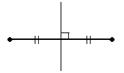
	Определение. Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к данному отрезку и проходящая через ее середину.
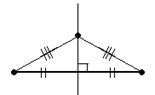
	Свойство серединного перпендикуляра. Любая точка с серединного перпендикуляра к отрезку равноудалена от его концов.
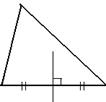
	Определение. Прямая, проходящая через середину стороны треугольника и перпендикулярная к ней, называется серединным перпендикуляром треугольника.

Серединные перпендикуляры треугольника обладают следующими свойствами.

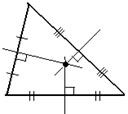
	1. Каждый треугольник имеет три серединных перпендикуляра. 2. Три серединных перпендикуляра треугольника пересекаются в одной точке. 3. Точка пересечения серединных перпендикуляров – центр описанной окружности.
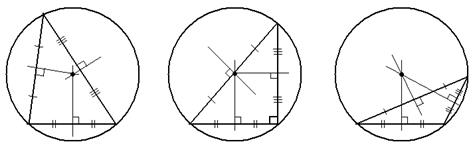
4. Если треугольник остроугольный, то серединные перпендикуляры пересекаются во внутренней точке треугольника. Если треугольник прямоугольный, то серединные перпендикуляры пересекаются на середине гипотенузы. Если треугольник тупоугольный, то серединные перпендикуляры пересекаются в точке, лежащей вне треугольника.

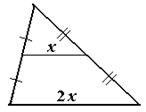
	Определение. Средней линией треугольника называется отрезок, соединяющий середины двух сторон треугольника.
Свойства средней линии треугольника. Средняя линия треугольника параллельна третьей стороне треугольника и равна половине ее длины.