АППАРАТУРНАЯ ФОРМА ЛИНИИ СЦИНТИЛЛЯЦИОННОГО g-СПЕКТРОМЕТРА

Структура преобразований функций распределения от первичного спектра j(Е) g-квантов, рожденных в источнике, до функции распределения по амплитудам импульсов f(A) на выходе детектора может быть представлена последовательностью, изображенной на рис. 1.12. Следует заметить, что после включения спектрометра и набора спектра на мониторе видно изображение спектра f(А) в виде гистограммы f(n), где n – номер канала анализатора, однозначно связанный с амплитудой импульса А.

Если полагать, что преобразование одной функции распределения в другую происходит мгновенно, т.е. каждый рожденный в источнике g-квант будет регистрироваться без помех со стороны других g-квантов[10], то вся последовательность преобразований может рассматриваться в виде цепочки статистически независимых процессов, и между f(A) и j(Е) можно установить однозначную связь

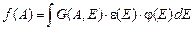, (1.5)

где функция G(A,E) называется функцией отклика спектрометра; она определяет плотность вероятности получить на выходе детектора импульс с амплитудой А, если в его чувствительный объем попал g-квант с энергией Е. Функция e(E) называется эффективностью спектрометра и характеризует вероятность g-кванту, рожденному в источнике с энергией Е, попасть в чувствительный объем детектора и провзаимодействовать там, передать энергию (или ее часть) быстрому электрону (или электронам).

Для моноэнергетического излучения, представляя j(E) в виде d-функции j(E) = d(E − E₀), получаем, учитывая свойство d-функции

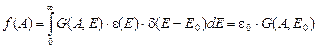, (1.6)

где e₀ = e(Е₀).

Полное поглощение энергии g-кванта в детекторе возможно при фотоэффекте, многократном комптоновском рассеянии внутри чувствительного объема, оканчивающемся тоже фотоэффектом и при образовании пар. Если при образовании пар аннигиляционные g-кванты покидают детектор, это отображается на аппаратурном распределении в виде соотвествующих пиков (см. рис. 1.13). Помимо первичного излучения в чувствительный объем детектора может попадать излучение, рассеянное вокруг детектора. Этот процесс тоже отображен в виде непрерывного распределения и небольшого пика, называемого пиком обратного рассеяния.

Крайний правый пик 1 на рис. 1.13 соответствует полному поглощению энергии первичного g-кванта Е₀ в чувствительном объеме детектора. Сюда не могут попасть импульсы с амплитудой, соответствующей энергии рассеянного в источнике или в защите кванта, все эти импульсы будут находиться левее пика полного поглощения (ППП). Поэтому функция описания ППП будет зависеть только от количества первичных g-квантов, которые достигли чувствительного объема детектора и провзаимодействовали там таким образом, что вся энергия оказалась переданной быстрым электронам. «Комптоновский край» распределения 2 на рис. 1.13 вычисляется по формуле (1.3), он соответствует максимально переданной электрону энергии, которая по лучается при рассеянии g-кванта на 180⁰ (назад). Пики 3 и 4 обусловлены полной потерей энергии падающего g-кванта за счет эффекта образования пар, за вычетом одного 3 или двух 4 аннигиляционных квантов, имеющих энергию по 0,511 МэВ и вылетевших из детектора. Пик обратного рассеяния 6 обусловлен попаданием в детектор g-квантов, отраженных на 180⁰ от конструкционных материалов (например, защитного домика). Энергия g-кванта, рассеянного на 180⁰, будет минимальна и равна

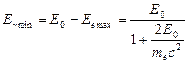. (1.7)

При взаимодействии g-квантов с окружающими материалами за счет фотоэффекта возникает характеристическое излучение этих материалов, которое регистрируется детектором и образует пик характеристического излучения (ПХИ). Энергия этого пика примерно равна энергии связи электрона на K-оболочке. Обычно ближе всего к детектору расположен защитный домик из свинца, поэтому в аппаратурном спектре должен быть ПХИ, соответствующий энергии связи на K-оболочке в свинце: E_K = 72 кэВ.

Если учесть, что эффект образования электрон-позитронных пар становится заметным при энергиях g-квантов более 5 МэВ, а энергии g-квантов, испускаемые большинством радионуклидов, измеряемых в пробах внешней среды, значительно меньше, пики однократного и двойного вылета в распределении амплитуд практически будут отсутствовать. Поэтому аппаратурная форма линии может быть представлена в виде суммы из быстроменяющейся вдоль оси амплитуд пиковой компоненты G_б(A,E₀) и сравнительно медленноменяющейся компоненты G_м(A,E₀), связанной с рассеянием g-квантов в источнике, в защите и с неполным поглощением энергии в детекторе (рис. 1.14).

Можно построить такой метод обработки аппаратурного спектра, что медленноменяющаяся компонента будет подавляться каким-либо математическим фильтром, а пиковая проходить сквозь фильтр. Такой способ реализуется, например, человеческим мозгом при поиске отдельных пиков на аппаратурном спектре. Тогда в качестве аппаратурной формы линии может служить G_б(A,E₀), в качестве эффективности регистрации – величина e_б(E₀), которая называется эффективностью спектрометра по пику полного поглощения энергии g-квантов, а вместо выражения (1.6) можно записать

f_б(A) = e_б(E₀)×G_б(A,E₀) или f_ППП(А) = e_ППП(Е₀)×G_ППП(A,E₀) . (1.8)

Эффективность спектрометра по пику полного поглощения e_ППП(E₀) – это вероятность того, что g-квант, рожденный в источнике с энергией Е₀, без всяких взаимодействий по пути попадет в чувствительный объем детектора и там передаст всю свою энергию быстрым электронам или, что фактически одно и то же, затратит всю энергию на образование фотонов видимого света. Таким образом, e_ППП(E₀) можно представить произведением независимых вероятностей

e_ППП(E₀) = e_б(E₀) = р₁(Е)×р₂(Е), (1.9)

где р₁(Е) – вероятность g-кванту попасть в детектор и провзаи-модействовать с его материалом в чувствительном объеме;

р₂(Е) – вероятность полной передачи энергии на образование фотонов.

Вероятность р₂(Е) иногда называют фотовкладом, который определяется как число взаимодействий с полным поглощением к числу всех взаимодействий g-квантов в детекторе. Численно фотовклад определяется как отношение площади под ППП к площади всего распределения. Представление e_ППП(E₀) в виде произведения вероятностей позволяет для простых геометрических форм источника и детектора рассчитать e_ППП(E). Для этого нужно знать значения линейных коэффициентов ослабления g-квантов в материалах источника и детектора для данной энергии (табулированные величины, имеются в справочниках) и провести измерения фотовклада р₂(Е) с образцовыми точечными непоглощающими источниками, учитывая тот факт, что р₂(Е) – характеристика детектора, не зависящая от источника; она может быть определена заранее раз и навсегда, в отличие от р₁(Е), которую нужно рассчитывать для каждой новой геометрии источника заново.

Аппаратурная форма линии G_ППП(A,E₀) может быть записана в аналитическом виде. Среднее число фотонов, образованных в сцинтилляторе в случае полного поглощения энергии, будет линейно связано с этой энергией: n_ф ~ k×E₀. Дальнейшая цепочка преобразований от n_ф к А состоит из статистически независимых элементов: n_ф ® число фотоэлектронов на фотокатоде ® число вторичных электронов на первом диноде ® число вторичных электронов на n-м диноде ® число электронов на аноде ® амплитуда А импульса на емкости анода. Из центральной предельной теоремы математической статистики следует, что функция распределения амплитуд импульсов в таком случае будет приближенно нормальной (гауссовой), т.е. пик полного поглощения должен иметь вид гауссиана

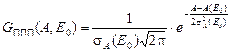, (1.10)

где А(Е₀) = k×Е₀; k = const; s_А(Е₀) – параметр ширины функции распределения амплитуд, характеризующий энергетическое разрешение спектрометра DА при энергии Е₀ (если связать DА с параметром гауссиана s_А, то DА = 2,35×s_А). Зависимости s_А(Е) и А(Е) могут быть получены в специальном градуировочном эксперименте с образцовыми точечными источниками.