ИЗМЕРЕНИЕ АППАРАТУРНЫХ РАСПРЕДЕЛЕНИЙ АМПЛИТУД

Для измерения аппаратурных распределений амплитуд применяются специальные электронные схемы – амплитудно-цифровые преобразователи (АЦП). При этом вся шкала возможных амплитуд разбивается на множество одинаковых отрезков шириной DА, которые нумеруются в порядке возрастания и называются каналами АЦП. Каждый канал имеет свой индивидуальный счетчик, и если на входе АЦП появился импульс с амплитудой А и величина А находится в пределах от n×DА до (n+1)×DА, то в счетчике n-го канала добавляется единица. После измерений в течение некоторого времени t_изм. в счетчиках будет накоплено столько зарегистрированных событий, сколько раз за это время амплитуда на выходе детектора попадала в интервал, соответствующий данному номеру счетчика или номеру канала АЦП (номеру канала анализатора). Таким образом, в результате измерений аппаратурного распределения получаем набор из целых чисел N_i, i = 1, 2, … , n, n - число каналов АЦП, т.е. гистограмму функции распределения. Каждое число N_i является случайной величиной и показывает, сколько раз за время измерений амплитуда импульса попадала в i-й канал.

В предыдущем параграфе было показано, что функция распределения амплитуд имеет вид набора пиковых компонент, соответствующих полной передаче энергии, на фоне медленно-

меняющихся компонент, соответствующих неполной передаче энергии. Поэтому, если из измеренного аппаратурного распределения выделить только пиковые составляющие, то энергиям первичных g-квантов будут соответствовать положения пиков на шкале амплитуд, а площади под пиками будут через эффективность регистрации e_ППП(Е) (см. формулу (1.15)) связаны с интенсивностями испускания g-линий источником. Таким образом, анализ аппаратурного распределения может быть сведен к определению положений пиков полного поглощения и площадей под ними. И положение ППП, и площадь под пиком определяются анализом измеренной гистограммы функции распределения амплитуд импульсов, т.е. анализом набора случайных величин N_i (рис. 1.15). Наиболее устойчивой характеристикой положения пика в этих условиях может служить положение центра тяжести пика (ЦТП)[12]. В качестве оценки площади под пиком, с учетом того, что быстроменяющаяся компонента функции отклика описывается гауссианом (1.10) с параметром ширины s_А, может служить разность (S_полн. – S_фон), где S_полн. – сумма отсчетов N_i в каналах расположения пика, а S_фон – площадь фоновой подложки под пиком, определяемая как площадь трапеции, высота которой соответствует ширине пика (обычно достаточно ± 3s_А от ЦТП, рис. 1.15, б), а основаниями служат средние значения фоновой компоненты справа N_R и слева N_L от пика (рис. 1.15, а).

Под фоновой компонентой подразумевается суммарная медленноменяющаяся компонента функции отклика. Фоновая компонента в районе расположения пика обычно аппроксимируется линейной функцией, как показано на рис. 1.15, а. Центр тяжести пика определяется после вычета фоновой составляющей на рис. 1.15, б. Очевидно, и площадь под пиком S_ППП, и положение его центра тяжести будут случайными величинами, поскольку определяются через случайные числа отсчетов N_i в каналах АЦП. Каждое N_i имеет пуассоновское распределение и суммы случайных пуассоновских величин − тоже пуассоновские величины. А для пуассоновских распределений и среднее значение, и дисперсия равны одному и тому же числу – параметру распределения, поэтому можно оценить случайную погрешность экспериментального определения площади под пиком. Вся площадь под аппаратурным распределением складывается в двух статистически независимых процессах – формировании пиковой (быстроменяющейся) компоненты и формировании фоновой (медленноменяющейся) компоненты. Для площади под пиком полного поглощения можно записать

S_ППП = S_полн. - S_фон, (1.11)

тогда оценка дисперсии площади пика D(S_ППП) будет равна[13]

D(S_ППП) = D(S_полн.) + D(S_фон) = S_полн. + S_фон = S_ППП +2S_фон , (1.12)

а среднеквадратичный разброс для площади ППП

s(S_ППП) = 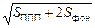. (1.13)

Следует отметить, что формулы (1.12), (1.13) приближенные, поскольку не учитывают еще дополнительной погрешности аппроксимации линии фоновой подложки и способа проведения этой линии, но для практической g-спектрометрии они вполне пригодны.