Геометрические параметры несущей поверхности (крыла)
Форма горизонтального и вертикального оперения самолета описывается теми же параметрами, что и форма крыла.
Форма крыла в плане появляется в результате компромисса между требованиями аэродинамики, прочности, технологии и т. п. и описывается отрезками прямых, кривых (второго и более высоких порядков) или их комбинацией. Обратите внимание на формы крыльев самолетов, показанных на рис. 7.2 (масштабы самолетов - разные).
|
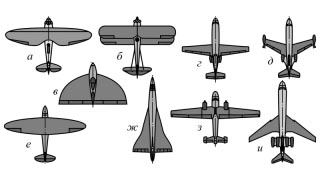
| Рис. 7.2. Различные формы в плане несущих поверхностей самолетов: а - АНТ-5; б - По-2; г - Як-40; д - HFB-320 (ФРГ); е - К-2; ж - Ту-144; з - Ан-28; и - Ил-62 |
Крыльям, форма в плане которых ограничивается простейшими кривыми второго порядка, иногда дают названия по названию соответствующей кривой: "эллиптическое" (эллипсовидное) крыло (рис. 7.2,е), "параболическое крыло с прямой задней кромкой" (рис. 7.2,в).
Крыльям более сложных очертаний иногда дают даже специальные названия: "серповидное" (форма крыла напоминает очертания серпа), "оживальное" ("готическое") (рис. 7.2,ж).
Для крыльев простых очертаний (рис. 7.3) основными геометрическими параметрами являются параметры, представленные на рис. 7.4.
Хорда (от греч.chorde - струна) - длина отрезка линии, ограниченного носиком и хвостиком сечения крыла вертикальной плоскостью в направлении полета. Обычно концевая хорда крыла самолета меньше корневой.
| 
|
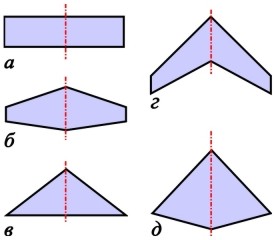
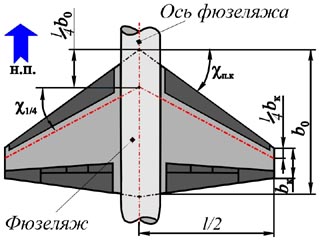
| Рис. 7.3. Простые формы крыла в плане: а - прямоугольное; б - трапециевидное; в - треугольное; г - стреловидное; д - ромбовидное | Рис. 7.4. Основные геометрические параметры крыла |
В практических расчетах по аэродинамике и динамике полета самолета пользуются средней аэродинамической хордойкрыла bA - (САX крыла). Для крыла произвольной формы в планесредняя аэродинамическая хорда определяется по формуле
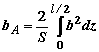
| где | S | - | площадь крыла, м² ; | |
| l | - | размах крыла, м; | ||
| b | - | текущая хорда крыла, м. |
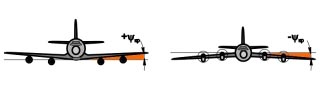
Поперечный угол крыла Ψкр, или так называемый угол поперечного V крыла, характеризует вид крыла спереди (рис. 7.5). Для современных самолетов значения угла Ψкр лежат в пределах от -5° до +5°.
|
| Рис. 7.5. К пояснению угла поперечного V крыла: а - Ил-86; б - Ту-144 |
Сужение крыла η оценивает степень трапециевидности крыла η = b0 /bк.
Очевидно, что для прямоугольного крыла (рис. 7.3,а) η = 1, для треугольного (рис. 7.3,в) и ромбовидного (рис. 7.3,д) η=.
Удлинение крыла λ характеризует отношение размаха к средней хорде и определяется соотношением λ = λ2/S.
Условно различают крылья малого и большого удлинения. Крыло малого удлинения (λ = 2¸3) - короткое, с относительно большими хордами, применяется на сверхзвуковых самолетах; крыло большого удлинения (λ = 6¸12) - длинное, с относительно малыми хордами, применяется на дозвуковых пассажирских (транспортных) самолетах.
У крыла прямой стреловидности (рис. 7.2,и) концевая хорда отнесена назад по потоку относительно корневой хорды крыла. У крыла обратной стреловидности (рис. 7.2,д) концевая хорда находится впереди по потоку относительно корневой хорды. У крыльев скоростных дозвуковых пассажирских самолетов угол стреловидности χ1/4 = 20¸35°, у крыльев самолетов, летающих на сверхзвуковых режимах, угол стреловидности по передней кромке χ= 20¸70°.
Профиль несущей поверхности - это форма сечения крыла плоскостью, параллельной плоскости симметрии самолета. Профилировка сечения крыла в основном определяет характер обтекания несущей поверхности воздушным потоком, спектр скоростей и, соответственно, эпюру давлений. Таким образом, аэродинамические характеристики крыла во многом зависят от профиля. В распоряжении проектировщиков имеются многотомные "Атласы профилей", в которых наряду с геометрическими параметрами профилей приведены их аэродинамические характеристики. Потребность в определенных аэродинамических характеристиках проектируемого самолета приводит проектировщика к выбору определенной серии профилей (симметричный или несимметричный профиль, с плоскими или криволинейными образующими и т. д.) крыла.
|
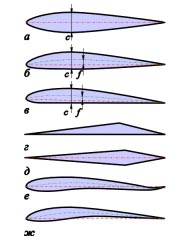
| Рис. 7.6. Некоторые формы (серии) профилей: |
Некоторые формы профилей представлены на рис. 7.6.
Помимо хорды b характерным линейным размером профиля является его максимальная толщинас и положение максимальной толщины по хорде, а также максимальная вогнутость профиля ƒ (расстояние от хорды до средней линии - геометрического места точек середин толщин профиля). Естественно, у симметричных профилей средняя линия совпадает с хордой. Обычно для характеристики профиля используются относительные величины:
относительная толщина
c= с/b·100%;
относительная кривизна
ƒ= f/b·100%.
Профилиодной серии (например, несимметричные двояковыпуклые) отличаются друг от друга значениями c и ƒ.
Относительная толщина современных профилей имеет очень широкий диапазон значений: c= 3¸8% - тонкие профили для крыльев сверхзвуковых самолетов; c= 8¸12% - профили средней толщины для скоростных дозвуковых самолетов; c= 12¸18% - толстые профили для нескоростных самолетов. Относительная кривизна современных профилей ƒ= 0¸3%.
В настоящее время большое внимание уделяется поиску форм профилей, обеспечивающих в спектре обтекания профиля наличие достаточно протяженной зоны с ламинарным течением потока в пограничном слое (ламинарные, или ламинаризированные, профили), что позволяет снизить лобовое сопротивление несущих поверхностей.
Суперкритические профили, имеющие относительно плоский контур верхней поверхности, позволяют увеличить Мкрит полета дозвукового самолета, т. е. отодвинуть эффект волнового кризиса и, увеличив таким образом крейсерскую скорость, повысить транспортную эффективность самолета.
На улучшение аэродинамических характеристик несущей поверхности (крыла) направлены и такие конструктивные решения, как геометрическая или аэродинамическая крутка крыла или их комбинация.
|
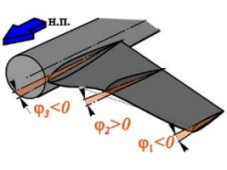
| Рис. 7.7. Геометрическая крутка крыла |
Геометрическая круткаобразуется на крыле, поперечные сечения которого набраны из профилей одной серии (с постоянными по размаху крыла значениями c и ƒ), установленных на различные углы φ по размаху (рис. 7.7), так что поверхность, образованная хордами профилей, оказывается не плоской.Аэродинамическая крутка образуется, когда вдоль размаха крыла на плоской серединной поверхности, образованной линиями хорд, в поперечных сечениях набраны профили различных серий (с переменными по размаху крыла значениями c и ƒ ).
Нетрудно заметить, что если крылья двух разных самолетов составлены из одинаковых профилей (одной серии, c1 = c2 и ƒ1 =ƒ2 ) и при этом равны их стреловидности по передней кромке и сужения (χ1п.к. = χ2п.к; η1=η2), то при соблюдении условия λ1 = λ2 крылья подобны (конгруэнтны). Таким образом, удлинение λ характеризует подобие крыльев.
Как мы отмечали выше, геометрическое подобие обтекаемых тел позволяет по модели (аналогу) получить аэродинамические характеристики проектируемого самолета.
|
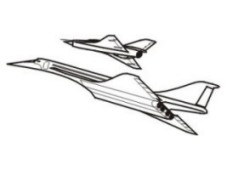
| Рис. 7.8. Сверхзвуковой пассажирский самолет Ту-144 и его аналог в полете |
Так, при проектировании сверхзвукового пассажирского самолета Ту-144 на базе легкого сверхзвукового истребителя МиГ-21 был построен самолет-аналог(рис. 7.8) с крылом сложной формы и профилировки, подобным крылу проектируемого самолета, что позволило не только смоделировать в реальном полете аэродинамику будущего Ту-144, но и решить другие проблемы.
Если в дополнение к записанным выше условиям геометрического подобия двух крыльев еще и S1 = S2, то крылья одинаковы.
Следует отметить, что не только геометрическое подобие агрегатов (частей) различных самолетов определяет аналогию их летных характеристик при одинаковых числах М полета, но также значения тяговооруженности P и удельной нагрузки на крыло p, которые, таким ообразом, также являются критериями при сравнении различных самолетов.
Дата добавления: 2014-12-24; просмотров: 3804;
