Задачи централизованного тестирования.
1. Пусть площадь равнобочной трапеции, описанной около круга, равна 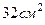 . Если острый угол при основании трапеции равен
. Если острый угол при основании трапеции равен 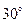 , то длина средней линии трапеции равна…
, то длина средней линии трапеции равна…
2. Если в равнобедренном прямоугольном треугольнике радиус вписанной окружности равен 4, то длина гипотенузы равна…
3. Если длины двух сторон треугольника равны 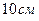 и
и 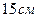 , то длина третьей стороны, лежащей против угла
, то длина третьей стороны, лежащей против угла 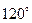 , равна…
, равна…
4. Если высота правильного треугольника равна  , то его периметр равен…
, то его периметр равен…
5. Если боковая сторона равнобедренного треугольника с острым углом при вершине равна 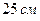 , а высота, проведенная к этой стороне, равна
, а высота, проведенная к этой стороне, равна  , то периметр треугольника равен…
, то периметр треугольника равен…
6. Если основания трапеции равны 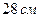 и
и  , а боковые стороны
, а боковые стороны 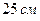 и
и 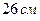 , то высота трапеции равна…
, то высота трапеции равна…
7. Пусть диагональ прямоугольной трапеции делит острый угол пополам, а высоту, опущенную из вершины тупого угла, на отрезки 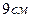 и
и 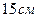 . Тогда периметр трапеции равен…
. Тогда периметр трапеции равен…
8. Из точки вне окружности проведена касательная длиной 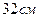 . Если расстояние от заданной точки до окружности равно
. Если расстояние от заданной точки до окружности равно  , то радиус окружности равен…
, то радиус окружности равен…
9. Точка касания окружности, вписанной в прямоугольный треугольник, делит гипотенузу в отношении 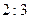 . Если меньший катет треугольника равен
. Если меньший катет треугольника равен 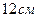 , то радиус вписанной окружности равен…
, то радиус вписанной окружности равен…
10. Стороны треугольника 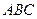 относятся как
относятся как 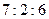 . Если разность между наибольшей и наименьшей стороной подобного ему треугольника
. Если разность между наибольшей и наименьшей стороной подобного ему треугольника 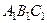 равна
равна 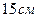 , то периметр треугольника
, то периметр треугольника 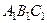 равен…
равен…
11. Пусть основание равнобедренного треугольника равно 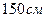 , а боковая сторона
, а боковая сторона  . Тогда расстояние между основаниями высот, проведенных к боковым сторонам, равно…
. Тогда расстояние между основаниями высот, проведенных к боковым сторонам, равно…
12. Если в треугольнике 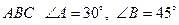 , а длина
, а длина 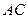 равна
равна  , то длина стороны
, то длина стороны 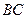 равна…
равна…
13. Пусть в окружности диаметром 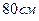 по одну сторону от центра проведены две параллельные хорды длиной
по одну сторону от центра проведены две параллельные хорды длиной 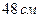 и
и 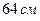 . Тогда расстояние между хордами равно…
. Тогда расстояние между хордами равно…
14. Пусть точка внутри угла, равного 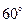 , удалена от его сторон на
, удалена от его сторон на 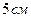 и
и 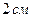 . Расстояние от вершины угла до этой точки равно…
. Расстояние от вершины угла до этой точки равно…
15. Если в окружности центральный угол на 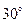 больше вписанного в окружность угла, опирающегося на ту же дугу, то дуга содержит…
больше вписанного в окружность угла, опирающегося на ту же дугу, то дуга содержит…
16. Пусть периметр прямоугольного треугольника равен 36, а радиус вписанной в него окружности равен 3,5. Тогда радиус описанной окружности равен… (В данной задаче не стоит находить длины сторон треугольника, так как такой треугольник не существует вообще(ошибка авторов), однако, если воспользоваться одной из теорем, то можно получить «правильный» ответ.)
17. Пусть в прямоугольный треугольник, катеты которого равны 10 и 15, вписан квадрат, имеющий с ним один общий угол. Тогда периметр квадрата равен…
18. Если хорды  и
и 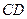 окружности пересекаются в точке
окружности пересекаются в точке 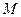 , длина отрезка
, длина отрезка 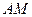 относится к длине отрезка
относится к длине отрезка 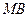 как
как  , длина хорды
, длина хорды 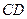 равна
равна 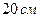 , длина отрезка
, длина отрезка  равна
равна 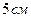 , то длина хорды
, то длина хорды  равна…
равна…
19. Если острый угол между диагоналями параллелограмма равен 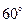 , их длины равны
, их длины равны 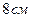 и
и 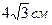 , то площадь параллелограмма равна…
, то площадь параллелограмма равна…
20. Если в двух подобных треугольниках длины меньших сторон равны 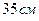 и
и 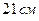 , а разность периметров равна
, а разность периметров равна 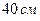 , то сумма периметров равна…
, то сумма периметров равна…
Ответы:
1.
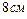
| 2. 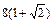
| 3. 
| 4. | 5.
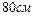
| 6.
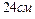
| 7.
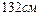
| 8.
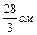
| 9.
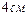
| 10.
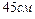
|
11.
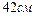
| 12. | 13.
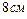
| 14. 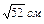
| 15.
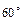
| 16. 7,25 | 17. | 18.

| 19. 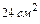
| 20. 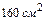
|
Дата добавления: 2014-12-22; просмотров: 1541;
