Свойства определенного интеграла.
1. 
.
2. 
.
3. Для любых чисел a, b и с имеет место равенство
.
4. Постоянный множитель можно вынести за знак определенного интеграла: 
.
5. Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их определенных интегралов: 
.
Далее будем полагать, что a<b.
6. Если функция 
всюду на отрезке 
, то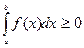 
.
7. Если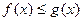 
всюду на отрезке , то 
.
8. Если функция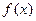 
интегрируема на , то 
.
9. Если М и m – соответственно, максимум и минимум функции 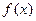на , то 
.
Дата добавления: 2014-12-04; просмотров: 833;