Выпуклость функции. Точки перегиба

Если в некотором интервале кривая расположена ниже любой своей касательной, то она называется выпуклой вверх, а если она расположена выше любой своей касательной, то называется выпуклой вниз в этом интервале.

Точкой перегиба называется точка на кривой, где меняется направление ее выпуклости.

Направление выпуклости кривой 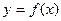характеризуется знаком второй производной 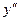: если в некотором интервале 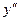>0, то кривая выпукла вниз, а если 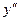<0, то кривая выпукла вверх в этом интервале.

Абсциссы точек перегиба кривой 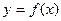, или графика функции f(x), являются точками экстремума производной 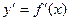. Поэтому их можно найти по следующему правилу:

1. Найти 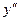и точки х, в которых 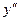=0 или не существует, а кривая непрерывна и которые лежат внутри области ее расположения.

2. Определить знак 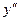слева и справа от каждой из этих точек. Исследуемая точка х будет абсциссой точки перегиба, если по разные стороны от нее 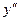имеет разные знаки.

Интервалы, где кривая выпукла вверх и где она выпукла вниз, определяются из условия, что их границами могут быть только абсциссы точек перегиба, точки разрыва и граничные точки области расположения кривой.