Наибольшее и наименьшее значение функции
Наибольшим значением функции называется самое большее, наименьшим значением – самое меньшее из всех ее значений.
Функция может иметь только одно наибольшее и только одно наименьшее значение или может не иметь их совсем. Нахождение наибольшего и наименьшего значений непрерывных функций основывается на следующих свойствах этих функций:
1) Если в некотором интервале (конечном или бесконечном) функция y=f(x) непрерывна и имеет только один экстремум и если это максимум (минимум), то он будет наибольшим (наименьшим) значением функции в этом интервале.
2) Если функция f(x) непрерывна на некотором отрезке [a, b], то она обязательно имеет на этом отрезке наибольшее и наименьшее значения. Эти значения достигаются ее или в точках экстремума, лежащих внутри отрезка, или на границах этого отрезка.
Для отыскания наибольшего и наименьшего значений на отрезке рекомендуется пользоваться следующей схемой:
1. Найти производную 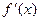 .
.
2. Найти критические точки функции, в которых 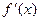 =0 или не существует.
=0 или не существует.
3. Найти значения функции в критических точках и на концах отрезка и выбрать из них наибольшее fнаиб и наименьшее fнаим.
При решении прикладных задач, в частности оптимизационных, важное значение имеют задачи на нахождение наибольшего и наименьшего значений (глобального максимума и глобального минимума) функции на промежутке Х. Для решения таких задач следует, исходя из условия, выбрать независимую переменную и выразить исследуемую величину через эту переменную. Затем найти искомое наибольшее или наименьшее значение полученной функции. При этом интервал изменения независимой переменной, который может быть конечным или бесконечным, также определяется из условия задачи.
Пример. Резервуар, имеющий форму открытого сверху прямоугольного параллелепипеда с квадратным дном, нужно вылудить внутри оловом. Каковы должны быть размеры резервуара при его емкости 108 л. воды, чтобы затраты на его лужение были наименьшими?
Решение. Затраты на покрытие резервуара оловом будут наименьшими, если при данной вместимости его поверхность будет минимальной. Обозначим через адм – сторону основания, bдм – высоту резервуара. Тогда площадь S его поверхности равна
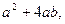
а объем
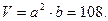
Отсюда
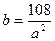 и
и 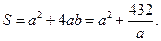
Полученное соотношение устанавливает зависимость между площадью поверхности резервуара S (функция) и стороной основания а (аргумент). Исследуем функцию S на экстремум. Найдем первую производную 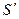 , приравняем ее к нулю и решим полученное уравнение:
, приравняем ее к нулю и решим полученное уравнение:
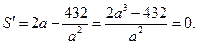
Отсюда а = 6. 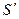 (а) > 0 при а > 6,
(а) > 0 при а > 6, 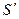 (а) < 0 при а < 6. Следовательно, при а = 6 функция S имеет минимум. Если а = 6, то b = 3. Таким образом, затраты на лужение резервуара емкостью 108 литров будут наименьшими, если он имеет размеры 6дм х 6дм х 3дм.
(а) < 0 при а < 6. Следовательно, при а = 6 функция S имеет минимум. Если а = 6, то b = 3. Таким образом, затраты на лужение резервуара емкостью 108 литров будут наименьшими, если он имеет размеры 6дм х 6дм х 3дм.
Пример. Найти наибольшее и наименьшее значения функции 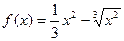 на промежутке
на промежутке 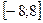 .
.
Решение: Заданная функция непрерывна на всей числовой оси. Производная функции
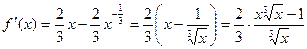 .
.
Производная 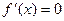 при
при 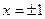 и
и 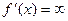 при
при 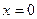 . Вычислим значения функции в этих точках:
. Вычислим значения функции в этих точках:
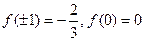 .
.
Значения функции на концах заданного промежутка равны 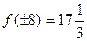 . Следовательно, наибольшее значение функции равно
. Следовательно, наибольшее значение функции равно 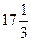 при
при 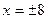 , наименьшее значение функции равно
, наименьшее значение функции равно 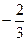 при
при 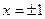 .
.
Вопросы для самопроверки
1. Сформулируйте правило Лопиталя для раскрытия неопределенностей вида 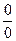 . Перечислите различные типы неопределенностей, для раскрытия которых может быть использовано правило Лопиталя.
. Перечислите различные типы неопределенностей, для раскрытия которых может быть использовано правило Лопиталя.
2. Сформулируйте признаки возрастания и убывания функции.
3. Дайте определение максимума и минимума функции.
4. Сформулируйте необходимое условие существования экстремума.
5. Какие значения аргумента (какие точки) называются критическими? Как найти эти точки?
6. Каковы достаточные признаки существования экстремума функции? Изложите схему исследования функции на экстремум с помощью первой производной.
7. Изложите схему исследования функции на экстремум с помощью второй производной.
8. Дайте определение выпуклости, вогнутости кривой.
9. Что называется точкой перегиба графика функции? Укажите способ нахождения этих точек.
10. Сформулируйте необходимый и достаточный признаки выпуклости и вогнутости кривой на заданном отрезке.
11. Дайте определение асимптоты кривой. Как найти вертикальные, горизонтальные и наклонные асимптоты графика функции?
12. Изложите общую схему исследования функции и построения ее графика.
13. Сформулируйте правило нахождения наибольшего и наименьшего значений функции на заданном отрезке.
Дата добавления: 2014-12-05; просмотров: 3113;
