Пример. .
Метод интегрирования подстановкой (заменой переменной)
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (т. е. подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся.
Пусть требуется вычислить интеграл 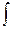 f(x) dx. Сделаем подстановку x = j(t), где j(t) – функция, имеющая непрерывную производную.
f(x) dx. Сделаем подстановку x = j(t), где j(t) – функция, имеющая непрерывную производную.
Тогда dx = j'(t)dt и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой
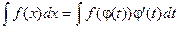
Эта формула также называется формулой замены переменных в неопределенном интеграле. После нахождения интеграла правой части этого равенства следует перейти от новой переменной интегрирования t назад к переменной х.
Иногда целесообразно подбирать подстановку в виде t = j(х), тогда 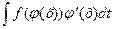 =
= 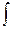 f(t)dt, где t =j(х). Другими словами, формулу можно применять справа налево.
f(t)dt, где t =j(х). Другими словами, формулу можно применять справа налево.
Пример. Найти 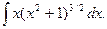
Замена 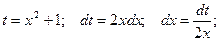 Получаем:
Получаем:
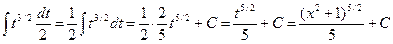 .
.
Дата добавления: 2014-12-05; просмотров: 1007;
