Определенный интеграл

Литература [1], [2],[3],[7],[15],[17],[19],[20],[21],[22].

Пусть на отрезке [a, b] задана непрерывная функция f(x).

y

M

m

0 a x_i b x

Обозначим m и M наименьшее и наибольшее значение функции на отрезке [a, b]. Разобьем отрезок [a, b] на части (не обязательно одинаковые) n точками.

x₀ < x₁ < x₂ < … < x_n

Тогда

x₁ – x₀ = Dx₁, x₂ – x₁ = Dx₂, … ,x_n – x_n-1 = Dx_n;

На каждом из полученных отрезков найдем наименьшее и наибольшее значение функции.

[x₀, x₁] ® m₁, M₁; [x₁, x₂] ® m₂, M₂; … [x_n-1, x_n] ® m_n, M_n.

Составим суммы:

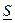_n = m₁Dx₁ + m₂Dx₂ + … +m_nDx_n =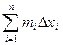

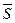_n = M₁Dx₁ + M₂Dx₂ + … + M_nDx_n =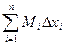

Сумма 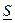называется нижней интегральной суммой, а сумма 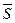– верхней интегральной суммой.

Т.к.

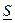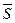m_i £ M_i, то _n £ _n,

а m(b – a) £ 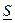_n £ 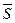_n £ M(b – a)

Внутри каждого отрезка выберем некоторую точку e.

x₀ < e₁ < x₁, x₁ < e < x₂, … , x_n-1 < e < x_n.

Найдем значения функции в этих точках и составим выражение, которое называется интегральной суммой для функции f(x) на отрезке [a, b].

S_n = f(e₁)Dx₁ + f(e₂)Dx₂ + … + f(e_n)Dx_n =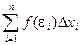

Тогда можно записать: m_iDx_i £ f(e_i)Dx_i £ M_iDx_i.

Следовательно,

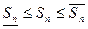
Геометрически это представляется следующим образом: график функции f(x) ограничен сверху описанной ломаной линией, а снизу – вписанной ломаной.

Обозначим maxDx_i – наибольший отрезок разбиения, а minDx_i – наименьший. Если maxDx_i® 0, то число отрезков разбиения отрезка [a, b] стремится к бесконечности.

Если 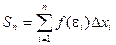, то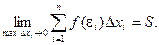

Определение. Если при любых разбиениях отрезка [a, b] таких, что maxDx_i® 0 и произвольном выборе точек e_i интегральная сумма 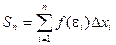стремится к пределу S, который называется определенным интегралом от f(x) на отрезке [a, b].

Обозначение: 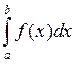, а – нижний предел, b – верхний предел, х – переменная интегрирования, [a, b] – отрезок интегрирования.

Определение.Если для функции f(x) существует предел

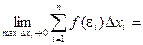
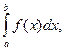
то функция называется интегрируемой на отрезке [a, b].

Также верны утверждения:

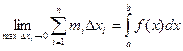
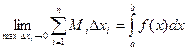
Теорема. Если функция f(x) непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.