Интегрирование рациональных дробей

Дробно-рациональной функцией (или рациональной дробью)называется функция, равная отношению двух многочленов, т. е. f(x) = 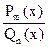, где P_m(x) –многочлен степени т, a Q_n(x) — многочлен сте­пени п.

Рациональная дробь называется правильной,если степень числите­ля меньше степени знаменателя, т. е. т < п; в противном случае (если т 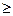п) рациональная дробь называется неправильной.

Всякую неправильную рациональную дробь 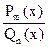можно, пу­тем деления числителя на знаменатель, представить в виде суммы многочлена L(x) и правильной рациональной дроби 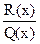, т.е.

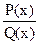= L(x) + .

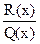Например, 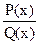= 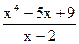– неправильная рациональная дробь. Раз­делим числитель на знаменатель в столбик.

Получим частное L(x) = х³ + 2х² + 4х + 3 и

остаток R(x) = 15. Следовательно, 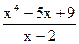= х³ + 2х² + 4х + 3 + + .

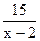Правильные рациональные дроби вида

I.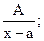

II.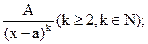

III. (корни знаменателя комплексные, т.е. p² - 4q < 0);

IV. 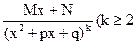, корни знаменателя комплексные),

где А, а, M, N, p, q – действительные числа, называются простейшими рациональными дробями I, II, III и IV типов.

Найдем интегралы от простейших рациональных дробей.

1. 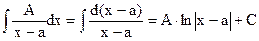(формула (2) из таблицы интегралов);

2.

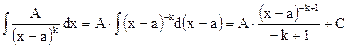
(формула (1));

3. Рассмотрим интеграл J = .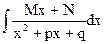

Выделив в знаменателе полный квадрат, получим:

J = ,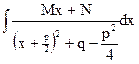

причем 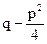> 0. Сделаем подстановку 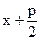= t. Тогда
x = , dx = dt. Положим 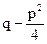= а². Следовательно, используя формулы (2) и (15) таблицы интегралов, получаем

J = = =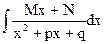

= =

= ,

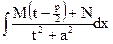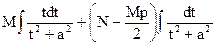т.е. возвращаясь к переменной х,

J= = = .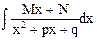

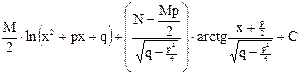Рассмотрим общее правило интегрирования рациональных дробей.

1. Если дробь неправильна, то представить ее в виде суммы многочлена и правильной дроби

2. Разложив знаменатель правильной рациональной дроби на множители, представить ее в виде суммы простейших рациональных дробей;

3. Проинтегрировать многочлен и полученную сумму простейших дробей.

Отметим, что любая рациональная функция интегрируется в элементарных функциях.

Пример.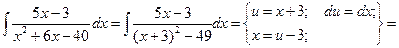

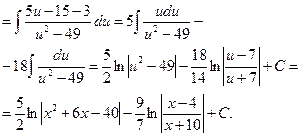
Вопросыдля самопроверки

1. Сформулируйте определение первообразной.
2. Каковы основные свойства неопределенного интеграла?
3. Запишите формулу интегрирования по частям.
4. Объясните правило разложения рациональной дроби на простейшие.