Свойства неопределенного интеграла
1. Дифференциал от неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции
2. Неопределенный интеграл от дифференциала некоторой функция равен сумме этой функции и произвольной постоянной:
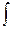 dF{x)= F(x) + С.
dF{x)= F(x) + С.
3. Постоянный множитель можно выносить за знак интеграла:
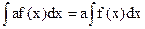 , а ≠ 0 – постоянная.
, а ≠ 0 – постоянная.
4. Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от слагаемых функций:
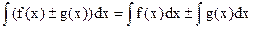 .
.
5. (Инвариантность формулы интегрирования). Если 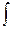 f{x)dx = F(x) + С, то и
f{x)dx = F(x) + С, то и 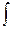 f(u)du = F(u) + С, где и — φ(x) — произвольная функция, имеющая непрерывную производную.
f(u)du = F(u) + С, где и — φ(x) — произвольная функция, имеющая непрерывную производную.
Таблица основных неопределенных интегралов
Пользуясь тем, что интегрирование есть действие, обратное дифференцированию, можно получить таблицу основных интегралов путем обращения соответствующих формул дифференциального исчисления (таблица дифференциалов) и использования свойств неопределенного интеграла.
Интегралы в приводимой ниже таблице называются табличными.
Таблица основных интегралов
| Интеграл | Значение | |
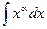
| 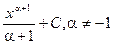
| |
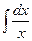
| 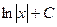
| |
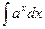
| 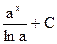
| |
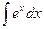
| ex + C | |
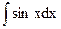
| -cosx + C | |
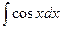
| sinx + C | |
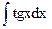
| -ln½cosx½+C | |
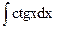
| ln½sinx½+ C | |
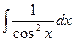
| tgx + C | |
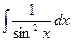
| -ctgx + C | |
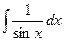
| 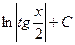
| |
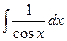
| 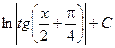
| |
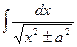
| ln 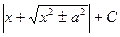
| |
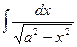
| arcsin 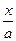 + C + C
| |
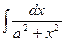
| 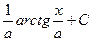
| |
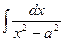
| 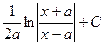
| |
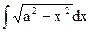
| 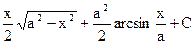
| |
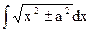
| 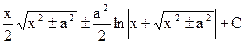
|
Дата добавления: 2014-12-05; просмотров: 1204;
