Метод интегрирования по частям
Пусть u = u(x), v = v(x) – функции, имеющие непрерывные производные. Тогда d(uv) = udv + vdu.
Интегрируя это равенство, получим
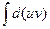 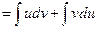 или или 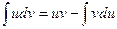 . .
|
Порученная формула называется формулой интегрирования по частям.Она дает возможность свести вычисление интеграла 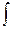 udv к вычислению интеграла
udv к вычислению интеграла 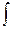 vdu, который может оказаться существенно более простым, чем исходный.
vdu, который может оказаться существенно более простым, чем исходный.
Интегрирование по частям состоит в том, что подынтегральное выражение заданного интеграла представляется каким-либо образом в виде произведения двух сомножителей и и dv (это, как правило, можно осуществить несколькими способами); затем, после нахождения v и du, используется формула интегрирования по частям. Иногда эту формулу приходится использовать несколько раз.
Укажем некоторые типы интегралов, которые удобно вычислять методом интегрирования по частям.
1. Интегралы вида 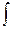 P(x)ekx dx,
P(x)ekx dx, 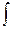 Р(х)× sin kxdx,
Р(х)× sin kxdx, 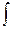 Р(х)×
Р(х)×
· cos kxdx, где Р(x) – многочлен, к – число. Удобно положить
и = Р(х), а за dv обозначить все остальные сомножители.
2. Интегралы вида 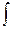 P(x)arcsinxdx,
P(x)arcsinxdx, 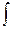 P(x)arcosxdx,
P(x)arcosxdx,
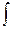 P(x)lnxdx,
P(x)lnxdx, 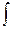 Р(х) arctgxdx,
Р(х) arctgxdx, 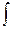 P(x)arcctgxdx. Удобно положить P(x) dx = dv, а за и обозначить остальные сомножители.
P(x)arcctgxdx. Удобно положить P(x) dx = dv, а за и обозначить остальные сомножители.
3. Интегралы вида 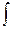 еах× sin bxdx,
еах× sin bxdx, 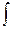 еах × cos bxdx, где а и b – числа.
еах × cos bxdx, где а и b – числа.
За u можно принять функцию и = еах.
Пример. 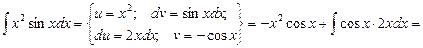
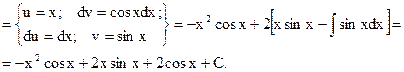
Дата добавления: 2014-12-05; просмотров: 1466;
