Экстремум функции
Значение функции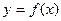 
в точке хо называется максимумом (минимумом), если оно является наибольшим (наименьшим) по сравнению с ее значениями во всех достаточно близких точках слева и справа от хо.
Функция может иметь экстремум (максимум или минимум) только в тех точках, которые лежат внутри области определения функции и где ее производная равна нулю или не существует. Такие точки называются критическими.
В соответствующих точках графика функции касательная параллельна оси абсцисс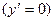 
, или оси ординат 
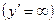или нет определенной касательной (например, как в угловой точке).
Точками экстремума являются все точки, где функция меняет свое поведение и непрерывна.
Точки, при переходе через которые аргумента х возрастание функции сменяется на убывание, являются точками максимума, а точки, при переходе через которые аргумента х убывание функции сменяется на возрастание, являются точками минимума.
Поскольку поведение функции характеризуется знаком ее производной, то функция будет иметь экстремум в тех точках, где ее производная меняет свой знак, а сама функция непрерывна.
Отсюда вытекает следующее правило исследования функции на экстремум.
Чтобы найти точки экстремума функции 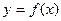, в которых она непрерывна, нужно:
1. Найти производную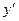 
и критические точки, в которых 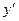=0 или не существует, а сама функция непрерывна, и которые лежат внутри области определения функции.
2а. Определить знак 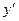слева и справа от каждой критической точки.
Если при переходе аргумента х через критическую точку хо:
1) 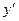меняет знак с + на -, то хо есть точка максимума;
2) 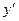меняет знак с - на +, то хо есть точка минимума;
3) 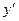не меняет знака, то в точке хо нет экстремума.
Иногда проще исследовать критические точки, где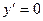 
, по знаку второй производной, - вместо правила 2а можно пользоваться следующим правилом:
2б. Найти вторую производную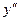 
и определить ее знак в каждой критической точке.
Если в критической точке хо, где :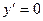
1) 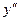>0, то хо есть точка максимума;
2) 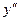<0, то хо есть точка минимума;
3) 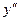=0, то вопрос о наличии экстремума в точке хо остается открытым. Такую критическую точку, как и всякую другую, можно исследовать по правилу 2а.
Далее следует найти экстремумы функции, т.е. вычислить значения функции в найденных точках экстремума.
Дата добавления: 2014-12-05; просмотров: 1360;