Применение производной к вычислению пределов.
Кроме элементарных способов, весьма эффективным средством для нахождения предела функции в тех случаях, когда аргумент неограниченно возрастает или стремится к значению, которое не входит в область определения функции, является правило Лопиталя.
Теорема. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных, если он существует или равен бесконечности.
Итак, если имеются неопределенности вида 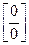 или
или 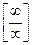 , то
, то
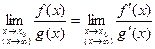 .
.
Обращаем внимание, что в правой части формулы берется отношение производных, а не производная отношения.
Пример. Найти: а) 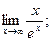 б)
б) 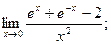 в)
в) 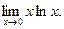
Решение. а) Имеем неопределенность вида 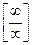 . Применяя правило Лопиталя, получим:
. Применяя правило Лопиталя, получим:
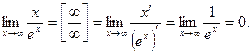
б) 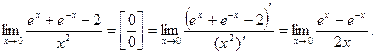
Неопределенность вида 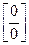 по-прежнему сохраняется. Применим правило Лопиталя еще раз:
по-прежнему сохраняется. Применим правило Лопиталя еще раз:
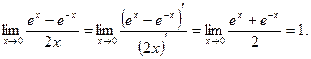
в) Имеем неопределенность вида 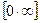 . Переписываем данное выражение в виде
. Переписываем данное выражение в виде
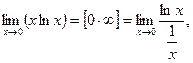

получим неопределенность вида 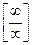 . Применяя правило Лопиталя, получим
. Применяя правило Лопиталя, получим
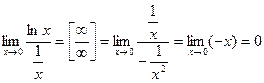 .
.
Дата добавления: 2014-12-05; просмотров: 7471;
