Понятие дифференциала функции, его геометрический смысл
Пусть функция 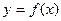 дифференцируема на отрезке
дифференцируема на отрезке 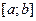 . Производная этой функции в некоторой точке
. Производная этой функции в некоторой точке 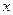 отрезка
отрезка 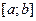 определяется равенством:
определяется равенством: 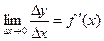 . Тогда, по теореме о связи функции, её предела и бесконечно малой функции, можно записать
. Тогда, по теореме о связи функции, её предела и бесконечно малой функции, можно записать 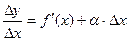 , где
, где 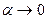 при
при 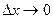 , или
, или 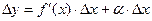 .
.
Приращение функции 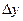 состоит из двух слагаемых, из которых первое есть так называемая главная часть приращения, линейная относительно
состоит из двух слагаемых, из которых первое есть так называемая главная часть приращения, линейная относительно 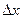 .
.
Дифференциалом функции 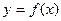 в точке
в точке 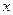 называется главная часть её приращения, которая равна произведению производной функции на приращение аргумента, и обозначается
называется главная часть её приращения, которая равна произведению производной функции на приращение аргумента, и обозначается 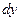 или
или 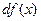 :
: 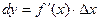 .
.
Дифференциал 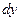 называют также дифференциалом первого порядка.
называют также дифференциалом первого порядка.
Дифференциал независимой переменной равен приращению этой переменной: 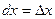 и тогда
и тогда 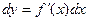 , дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Пример 1. Найти дифференциал функции 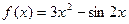 .
.
Решение: По формуле 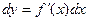 находим
находим
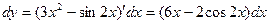 .
.
Основные теоремы о дифференциалах. Таблица дифференциалов.
Теорема 1. Дифференциал суммы, произведения и частного двух дифференцируемых функций определяется формулами:
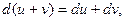
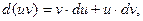
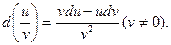
Теорема 2.Дифференциал сложной функции равен произведению производной этой функции по промежуточной переменной на дифференциал этой промежуточной переменной
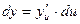 .
.
Таблица дифференциалов
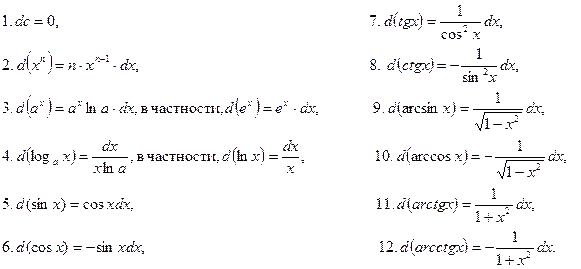
Дата добавления: 2014-12-05; просмотров: 1685;
