Производные высших порядков неявно заданной функции

Пусть функция у = f(х) задана неявно в виде уравнения F(х; у) = 0.

Продифференцировав это уравнение по х и, разрешив полученное уравнение относительно у', найдем производную первого порядка (первую производную). Продифференцировав по х первую производную, получим вторую производную от неявной функции. В нее войдут х, у и у'. Подставляя уже найденное значение у' в выражение второй производной, выразим y” через х и у.

Аналогично поступаем для нахождения производной третьего (и дальше) порядка.

Пример 13. Найти 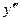, если х² + y² = 1.

Решение: Дифференцируем уравнение х² + y² – 1 = 0 по х:

2x + 2y × y¢ = 0.

Отсюда

.

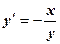Далее имеем:

у” = ,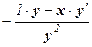

т.е.

у” = ,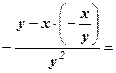

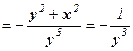(т.к. х² + y² = 1),следовательно,

.

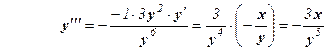Вопросы для самопроверки

1. Что называется средней скоростью изменения функции, скоростью изменения функции?

2. Сформулируйте определение производной. Каков ее механический и геометрический смысл?

3. Чему равна производная от постоянной величины? от аргумента?

4. Сформулируйте правила дифференцирования суммы, произведения и частного двух функций.

5. Сформулируйте правило дифференцирования сложной функции.

6. Приведите формулы дифференцирования основных элементарных функций.

7. Сформулируйте правило логарифмического дифференцирования.

8. Приведите формулу дифференцирования обратной функции.

9. Сформулируйте правило дифференцирования неявной функции.

10. Что называется производной второго порядка? Каково механическое истолкование производной второго порядка?