Производная неявно заданной функции
Если функция задана уравнением у = f (х), разрешенным относительно у, то функция задана в явном виде (явная функция).
Под неявным заданием функции понимают задание функции в виде уравнения F(х; у) = 0, не разрешенного относительно у.
Всякую явно заданную функцию у = f (х) можно записать как неявно заданную уравнением f (х) – у = 0, но не наоборот.
Если неявная функция задана уравнением F(х; у) = 0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по х, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'.
Производная неявной функции выражается через аргумент х и функцию у.
Пример 6. Найти производную функции у, заданную уравнением
x3 + y3 – 3xy = 0.
Решение: Функция у задана неявно. Дифференцируем по х равенство
x3 + y3 – 3xy = 0. Из полученного соотношения 3x2 + 3y2 × у' – 3(1× y + x× у') = 0
следует, что y2 × у' – x× у' = y – x2, т.е.
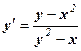 .
.
Таблица производных
На практике чаще всего приходится находить производные от сложных функций. Поэтому в приведенной ниже таблице формул дифференцирования аргумент «х» заменен на промежуточный аргумент «u».
- (с)¢ = 0;
- (
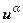 )¢ =
)¢ = 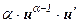 ;
; -
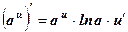 , в частности,
, в частности, 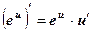 ;
; -
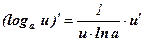 , в частности,
, в частности, 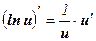 ;
; - (sin u)¢ = cos u × u¢;
- (cos u)¢ =
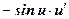 ;
; - (tg u)¢
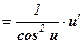 ;
; - (сtg u)¢
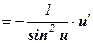 ;
; - (arcsin u)¢ =
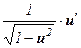 ;
; - (arccos u)¢ =
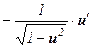 ;
; - (arctg u)¢ =
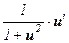 ;
; - (arcctg u)¢
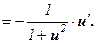
Дата добавления: 2014-12-05; просмотров: 5932;
