Производная обратной функции
Пусть 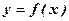 и
и 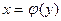 - взаимно обратные функции.
- взаимно обратные функции.
Теорема 6. Если функция 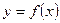 строго монотонна на интервале
строго монотонна на интервале 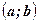 и имеет неравную нулю производную
и имеет неравную нулю производную 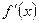 в произвольной точке этого интервала, то обратная ей функция
в произвольной точке этого интервала, то обратная ей функция 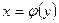 также имеет производную
также имеет производную 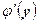 в соответствующей точке, определяемую равенством
в соответствующей точке, определяемую равенством 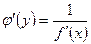 или
или 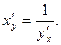
Таким образом, производная обратной функции равна обратной величине производной данной функции.
Правило дифференцирования обратной функции записывают так:
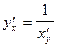 или
или 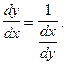
Пример 5. Пользуясь правилом дифференцирования обратной функции, найти производную y'x для функции 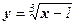 .
.
Решение: Обратная функция 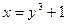 имеет производную
имеет производную 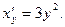
Следовательно, 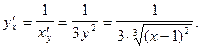
Дата добавления: 2014-12-05; просмотров: 989;
