Правила дифференцирования.
1. 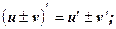
2. 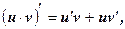 в частности,
в частности, 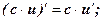
3. 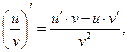 в частности,
в частности, 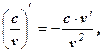
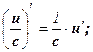
4. 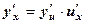 , если у =
, если у = 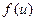 ,
, 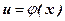 ;
;
5. 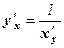 , если
, если 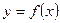 и
и 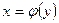 .
.
Для вычисления производных надо знать лишь правила дифференцирования и формулы производных основных элементарных функций, строго соблюдать эти правила при выполнении упражнений.
Пример 7. Найти производную функции у = 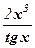 .
.
Решение: у' = 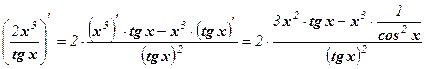 .
.
В процессе решения использованы правила 2, 3 и формулы 2, 7.
Пример 8. Найти производную функции 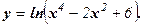
Решение: 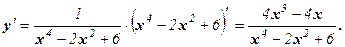
Пример 9. Найти производную функции у = cos 2x.
Решение: (cos 2x)¢ = - sin 2x × (2x)¢ = - 2sin 2x.
Пример 10. Найти производные функций:
1) y = arccos x2; 2) y =x× arctg x.
Решение:
1) (arccos x2)¢ = 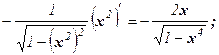
2) (x× arctg x)¢ = x¢× arctg x + x × (arctg x)¢ = arctg x + 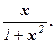
Пример 11. Найти производную функции у = cos(ln32x).
Решение: у' = 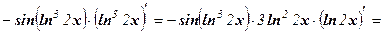
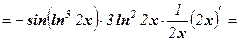
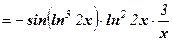 .
.
Решение с пояснениями: данную функцию можно представить следующим образом: у = cos u, u = t3, t = ln z, z = 2x. Производную сложной функции найдем по правилу 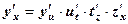 (здесь промежуточных аргументов три):
(здесь промежуточных аргументов три):
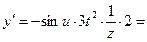
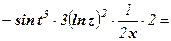
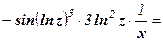
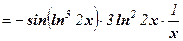 .
.
Окончательно 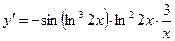 .
.
Дата добавления: 2014-12-05; просмотров: 1288;
