Производные высших порядков явно заданной функции
Производная у' = f '(х) функции у = f (x) есть также функция от х и называется производной первого порядка.
Если функция f '(х) дифференцируема, то ее производная называется производной второго порядка и обозначается у" (или f ¢¢(x), 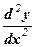 ,
, 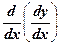 ,
, 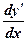 ). Итак,
). Итак,
у" = (y¢ )¢.
Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается у'" (или f¢¢¢(x), 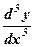 , …). Итак, у'" = (y¢¢)¢.
, …). Итак, у'" = (y¢¢)¢.
Производной n -го порядка (или n -й производной) называется производная от производной (n - 1) порядка: у(n) = (y(n – 1))¢ .
Производные порядка выше первого называются производными высших порядков.
Начиная с производной четвертого порядка, производные обозначают римскими цифрами или числами в скобках (у V или у(5) - производная пятого порядка).
Пример 12. Найти производную 13-го порядка функции у = sin x.
Решение: у' = (sin x)¢ = cos x = 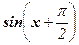 ,
,
у" = (y¢)¢ = (cos x)¢ = - sin x = 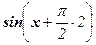 ,
,
у'" = (y¢¢)¢ = (- sin x)¢ = - cos x = 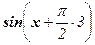 ,
,
……………………
у(13) = 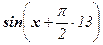
Дата добавления: 2014-12-05; просмотров: 1559;
