Производная сложной функции. Пусть у = и тогда у = f( (x)) — сложная функция с промежуточным аргументом и и независимым аргументом х.
Пусть у = 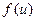 и
и 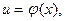 тогда у = f(
тогда у = f( 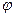 (x)) — сложная функция с промежуточным аргументом и и независимым аргументом х.
(x)) — сложная функция с промежуточным аргументом и и независимым аргументом х.
Теорема 5. Если функция 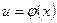 имеет производную
имеет производную 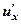 в точке
в точке 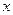 , а функция
, а функция 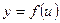 имеет производную
имеет производную 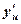 в соответствующей точке
в соответствующей точке 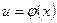 , то сложная функция у = f(
, то сложная функция у = f( 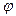 (x)) имеет производную
(x)) имеет производную 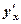 в точке
в точке 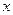 , которая находится по формуле
, которая находится по формуле
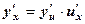 .
.
Итак, для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу.
Это правило остается в силе, если промежуточных аргументов несколько. Так, если 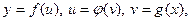 то
то 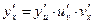 .
.
Пример 3. Найти производную функции 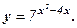
Решение: Используя формулу производной сложной функции и формулу производной показательной функции, находим
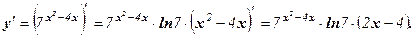
Пример 4. Найти производную функции 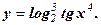
Решение: Данная функция является сложной. Ее можно представить в виде цепочки «простых» функций: у = u3, где u = 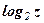 , где z =
, где z = 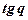 , где q = х4. По правилу дифференцирования сложной функции
, где q = х4. По правилу дифференцирования сложной функции 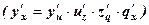 получаем:
получаем:
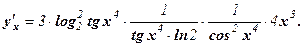
Дата добавления: 2014-12-05; просмотров: 1176;
