Определение производной; ее механический и геометрический смысл
Производной функции у = f(x) в точке 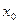 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю. Обозначают одним из символов:
называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю. Обозначают одним из символов: 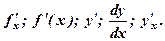
Итак, по определению
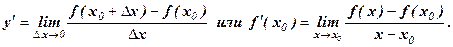
Производная функции 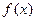 есть некоторая функция
есть некоторая функция 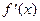 .
.
Функция у = 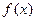 , имеющая производную в каждой точке интервала (а; b), называется дифференцируемой в этом интервале; операция нахождения производной функции называется дифференцированием.
, имеющая производную в каждой точке интервала (а; b), называется дифференцируемой в этом интервале; операция нахождения производной функции называется дифференцированием.
Значение производной функции у = 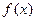 в точке
в точке 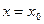 обозначается одним из символов:
обозначается одним из символов:
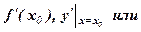
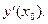
Пример 1. Найти производную функции у = с, с = const.
Решение: Значению 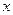 даем приращение
даем приращение 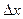 ; находим приращение функции
; находим приращение функции 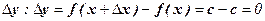 ; значит,
; значит, 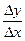 =
= 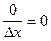 ;
;
следовательно, 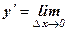
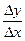 =
= 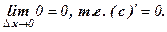
Пример 2.Найти производную функции у = х2.
Решение: Аргументу х даем приращение 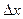 ; находим
; находим
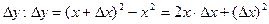 ;
;
составляем отношение 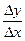 :
: 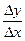 =
= 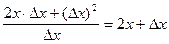 ; находим предел этого отношения:
; находим предел этого отношения: 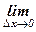
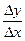 =
= 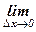
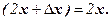
Таким образом, 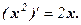
Механический смысл производной:
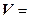
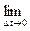
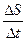 ,
,
или V = S¢t , т. е. скорость прямолинейного движения материальной точки в момент времени t есть производная от пути S по времени t.
Обобщая, можно сказать, что если функция у = f(x) описывает какой-либо физический процесс, то производная у' есть скорость протекания этого процесса. В этом состоит физический смысл производной.
Геометрический смысл производной:
Угловой коэффициент касательной 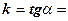
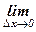
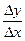 =
= 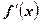 , т.е. производная
, т.е. производная 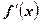 в точке x равна угловому коэффициенту касательной к графику функции у = f(x) в точке, абсцисса которой равна х.
в точке x равна угловому коэффициенту касательной к графику функции у = f(x) в точке, абсцисса которой равна х.
Уравнение касательной: у - 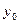 =
= 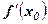 × (x - х0).
× (x - х0).
Прямая, перпендикулярная касательной в точке касания, называется нормалью к кривой.
Уравнение нормали: 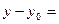
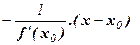 (если
(если 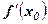
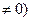 .
.
Дата добавления: 2014-12-05; просмотров: 2787;
