Непрерывность функции. Непрерывность функции в точке, на отрезке
Литература. [1], [2], [6], [7], [17].
Непрерывность функции в точке, на отрезке
Пусть функция у=f(x) определена в точке х0 и в некоторой окрестности этой точки.
Функция у=f(x) называется непрерывной в точке х0, если существует предел функции в этой точке и он равен значению функции в этой точке, т.е.
.
Это равенство означает выполнение трех условий:
1) функция f(x) определена в точке х0 и в ее окрестности;
2) функция f(x) имеет предел при 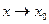 ;
;
3) предел функции в точке х0 равен значению функции в этой точке, т.е. выполняется равенство 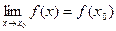 .
.
Так как 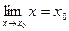 , то равенство
, то равенство 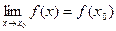 можно записать в виде
можно записать в виде
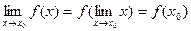 .
.
Это означает, что принахождении предела непрерывной функции f(x) можно перейти к пределу под знаком функции, то есть в функцию f(x) вместо аргумента х подставить его предельное значение х0.
Например, 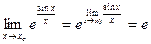 .
.
Сформулируем еще одно, второе определение непрерывности функции в точке: функция у=f(x) называетсянепрерывной в точке х0, если она определена в точке х0 и ее окрестности и выполняется равенство 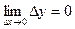 , т.е. бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
, т.е. бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Пример 13. Исследовать на непрерывность функцию 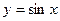 .
.
Решение: Функция 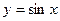 определена при всех
определена при всех 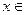 R. Возьмем произвольную точку х и найдем приращение
R. Возьмем произвольную точку х и найдем приращение 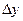 :
:
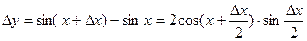 .
.
Тогда 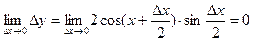 , так как произведение ограниченной функции и б.м.ф. есть б.м.ф. Согласно определению, функция
, так как произведение ограниченной функции и б.м.ф. есть б.м.ф. Согласно определению, функция 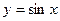 непрерывна в точке х.
непрерывна в точке х.
Функция у=f(x) называется непрерывной в интервале (а,b), если она непрерывна в каждой точке этого интервала.
Функция у=f(x) называется непрерывной на отрезке [а,b], если она непрерывна в интервале (а,b) и в точке х=а непрерывна справа(т.е. 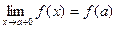 ), а в точке х=b непрерывна слева(т.е.
), а в точке х=b непрерывна слева(т.е. 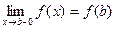 ).
).
Дата добавления: 2014-12-05; просмотров: 1259;
