Применение эквивалентных бесконечно малых функций к вычислению пределов
Для раскрытия неопределённостей вида 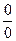 часто применяют принцип замены бесконечно малых эквивалентными и свойства эквивалентных бесконечно малых функций. Как известно, sinх ~ х при х → 0, tg x ~ х при х → 0. Приведем еще примеры эквивалентных б.м.ф.
часто применяют принцип замены бесконечно малых эквивалентными и свойства эквивалентных бесконечно малых функций. Как известно, sinх ~ х при х → 0, tg x ~ х при х → 0. Приведем еще примеры эквивалентных б.м.ф.
Пример 8. Покажем, что 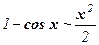 при х → 0.
при х → 0.
Решение: 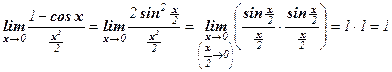 .
.
Пример 9. Найдем 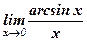 .
.
Решение: Обозначим arcsin х = t. Тогда х = sin t и t → 0 при х → 0. Поэтому 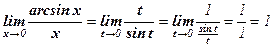 .
.
Следовательно, arcsin х ~ х при х → 0.
Таблица эквивалентных бесконечно малых
| 1. sin х ~ х, (х → 0); | 6. ех – 1 ~ х, (х → 0); |
| 2. tg х ~ х, (х → 0); | 7. ах – 1 ~ х ln а, (х → 0); |
| 3. arcsin х ~ х, (х → 0); | 8. ln(1 + х) ~ х, (х → 0); |
| 4. arctg х ~ х, (х → 0); | 9. loga (1 + х) ~ х loga е, (х → 0); |
5. 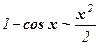 , (х → 0); , (х → 0);
| 10. (1 + х)k – 1 ~ k×x, k > 0, (х → 0);
в частности, 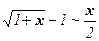 . .
|
Пример 10. Найти 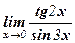 .
.
Решение: Так как tg 2х ~ 2х, sin 3х ~ 3х при х → 0,
то 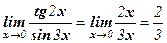 .
.
Пример 11. Найти 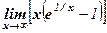 .
.
Решение: Обозначим 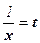 , из х → ∞ следует t → 0. Поэтому
, из х → ∞ следует t → 0. Поэтому
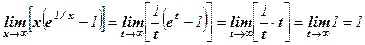 .
.
Пример 12.Найти 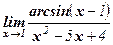 .
.
Решение: Так как arcsin (х – 1) ~ (х – 1) при х → 1, то
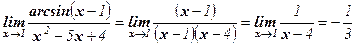 .
.
Дата добавления: 2014-12-05; просмотров: 2752;
