Свойства непрерывных функций

Свойства функций, непрерывных в точке:

1. Если функции f(x) и φ(x) непрерывны в точке х₀, то их сумма f(x)+φ(x), произведение f(x)φ(x) и частное 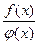(при условии 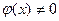) являются функциями, непрерывными в точке х_0.

2. Если функция у=f(x) непрерывна в точке х₀ и f(х₀)>0, то существует такая окрестность точки х₀, в которой f(х)>0.

3. Если функция f(и)>0 непрерывна в точке и₀, а функция и= φ(x) непрерывна в точке и₀= φ(x₀), то сложная функция у= f(φ(x)) непрерывна в точке х₀.

Свойство 3 может быть записано в виде 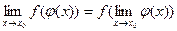, т.е. под знаком непрерывной функции можно переходить к пределу.

Функция у=f(x) называется непрерывной на промежутке Х, если она непрерывна в каждой точке этого промежутка. Все элементарные функции непрерывны в области их определения.

Свойства функций, непрерывных на отрезке:

1. Если функция у=f(x) непрерывна на отрезке [a,b], то она ограничена на этом отрезке.

2. Если функция у=f(x) непрерывна на отрезке [a,b], то она достигает на этом отрезке наименьшего значения т и наибольшего значения М (теорема Вейерштрасса).

3. Если функция у=f(x) непрерывна на отрезке [a,b] и значения ее на концах отрезка f(а) и f(b) имеют противоположные знаки, то внутри отрезка найдется точка 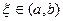такая, f(ξ)=0 (теорема Больцано-Коши).

Вопросы для самопроверки

1. Что называется числовой последовательностью?
2. Что называется пределом числовой последовательности?
3. Что называется пределом функции непрерывного аргумента?
4. Сформулируйте основные теоремы о пределах функции.
5. Какая переменная величина называется бесконечно малой? бесконечно большой? Какова зависимость между ними?
6. Сформулируйте основные свойства бесконечно малых величин.
7. Как найти предел дробно рациональной функци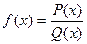и при 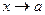, если 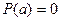и ?
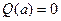8. Укажите приемы вычисления предела от простейших иррациональных функций.
9. Сформулируйте и напишите первый замечательный предел.
10. Сформулируйте и напишите второй замечательный предел.
11. Как сравнить между собой две бесконечно малые величины?
12. Какие две бесконечно малые величины называются эквивалентными, и каковы свойства эквивалентных бесконечно малых величин?
13. Что называется левосторонним пределом функции в данной точке? правосторонним пределом функции в данной точке?
14. Дайте определение непрерывности функции в точке; в интервале.
15. Какая точка называется точкой разрыва функции?
16. Что называется разрывом первого рода? второго рода?
17. Что называется скачком функции в точке разрыва?
18. Сформулируйте основные свойства функции непрерывной на отрезке.