Точки разрыва функции и их классификация

Точки, в которых нарушается непрерывность функции, называются точками разрываэтой функции. Если х=х₀ – точка разрыва функции у=f(x), то в ней не выполняется по крайней мере одно из условий первого определения непрерывности функции, а именно:

1. Функция определена в окрестности точки х_{0 ,} но не определена в самой точке х₀.

Например, функция 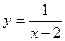не определена в точке х₀=2.

2. Функция определена в точке х₀ и ее окрестности, но не существует предела f(x) при .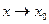

Например, функция 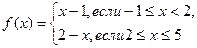определена в точке х₀=2, но имеет разрыв в этой точке, т.к. эта функция не имеет предела при 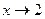: 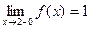, а .

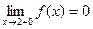3. Функция определена в точке х₀ и ее окрестности, существует предел 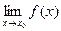, но этот предел не равен значению функции в точке х₀: .

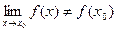Например, функция 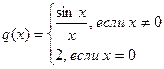. Здесь х₀=0 – точка разрыва: 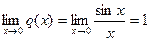, а q(0)=2.

Точка разрыва х₀ называется точкой разрыва первого родафункции у=f(x), если в этой точке существуют конечные пределы функции слева и справа, т.е. 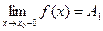и 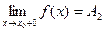. При этом:

а) если А₁=А₂, то точка х₀ называется точкой устранимого разрыва;

б) если 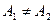, то точка х₀ называется точкой конечного разрыва. Величину 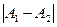называют скачком функциив точке разрыва первого рода.

Точка разрыва х₀ называется точкой разрыва второго рода функции у=f(x), если по крайней мере один из односторонних пределов не существует или равен бесконечности.

Для функции 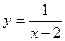точка х₀=2 – точка разрыва второго рода.

Для функции 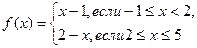х₀=2 является точкой разрыва первого рода, скачок функции равен .

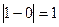Для функции 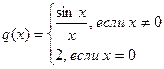х₀=0 является точкой устранимого разрыва первого рода. Положив q(x)=1 при х=0, разрыв устранится, функция станет непрерывной.