Сравнение бесконечно малых функций
Сумма, разность и произведение двух б.м.ф. есть функция бесконечно малая. Отношение же двух б.м.ф. может вести себя различным образом: быть конечным числом, быть бесконечно большой функцией, бесконечно малой или вообще не стремиться ни к какому пределу.
Две б.м.ф. сравниваются между собой с помощью их отношения.
Пусть a = a(х) и β = β(х) есть б.м.ф. при х → х0, т.е.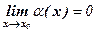 
и 
.
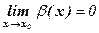1. Если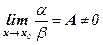 
(А Î R), то a и β называются бесконечно малыми одного порядка.
2. Если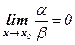 
, то a называется бесконечно малой более высокого порядка, чем β.
3. Если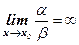 
, то a называется бесконечно малой более низкого порядка, чем β.
4. Если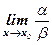 
не существует, то a и β называются несравнимыми бесконечно малыми.
Таковы же правила сравнения б.м.ф. при х → ± ∞, х → х0 ± 0.
Дата добавления: 2014-12-05; просмотров: 1008;