Основные теоремы о пределах
В приводимых теоремах будем считать, что пределы 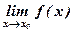 ,
,  существуют.
существуют.
Теорема 1. Предел суммы (разности) двух функций равен сумме (разности) их пределов
 .
.
Теорема справедлива для алгебраический суммы любого конечного числа функций.
Следствие. Функция может иметь только один предел при х → х0.
Теорема 2. Предел произведения двух функций равен произведению их пределов:
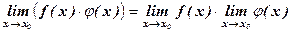 .
.
Теорема справедлива для произведения любого конечного числа функций.
Следствие 1. Постоянный множитель можно выносить за знак предела:
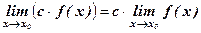 .
.
Следствие 2. Предел степени с натуральным показателем равен той же степени предела: 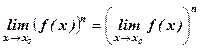 . В частности,
. В частности, 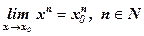 .
.
Теорема 3. Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю
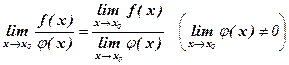 .
.
Пример 1. Вычислить 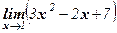 .
.
Решение:
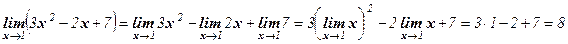 .
.
Пример 2. Вычислить 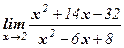 .
.
Решение: Здесь применить теорему о пределе дроби нельзя, т.к. предел знаменателя, при х → 2, равен 0. кроме того, предел числителя равен 0. В таких случаях говорят, что имеет неопределенность вида 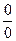 . Для ее раскрытия разложим числитель и знаменатель дроби на множители, затем сократим дробь на х – 2 ≠ 0 (х → 2, но х ≠ 2):
. Для ее раскрытия разложим числитель и знаменатель дроби на множители, затем сократим дробь на х – 2 ≠ 0 (х → 2, но х ≠ 2):
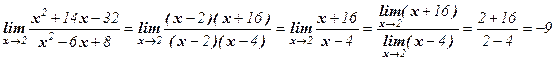 .
.
Пример 3. Вычислить 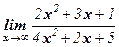 .
.
Решение: Здесь мы имеет дело с неопределенностью вида 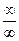 . Для нахождения предела данной дроби разделим числитель и знаменатель на х2.
. Для нахождения предела данной дроби разделим числитель и знаменатель на х2.
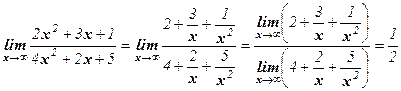 .
.
Функция 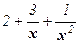 есть сумма числа 2 и б.м.ф., а функция
есть сумма числа 2 и б.м.ф., а функция 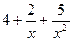 есть сумма числа 4 и б.м.ф., поэтому
есть сумма числа 4 и б.м.ф., поэтому
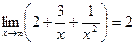 ,
, 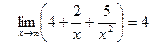 .
.
Дата добавления: 2014-12-05; просмотров: 1743;
