Предел функции в точке

Пусть функция у = f(х) определена в некоторой окрестности точки х₀, кроме, быть может, самой точки х₀.

Число А называется пределом функции у = f(х) в точке х₀ (или при х → х₀), если для любой последовательности допустимых значений аргумента х_n, n Î N (х_n ≠ х₀), сходящейся к х₀ (т.е. 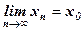), последовательность соответствующих значений функции f(х_n), n Î N, сходится к числу А (т.е. ).

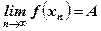В этом случае пишут 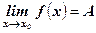или f(х) → А при х → х₀. Геометрический смысл предела функции: 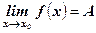означает, что для всех точек х, достаточно близких к точке х₀, соответствующие значения функции как угодно мало отличаются от числа А.