Числовая последовательность. Под числовой последовательностью x1, x2, x3, , xn, понимается функция , заданная на множестве N натуральных чисел

Под числовой последовательностью x₁, x₂, x₃, …, x_n, … понимается функция 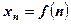^, заданная на множестве N натуральных чисел. Кратко последовательность обозначается в виде {х_n} или х_n, n Î N. Число x₁ называется первым членом (элементом) последовательности, x₂ – вторым,..., х_n – общим или n-м членом последовательности.

Чаще всего последовательность задается формулой ее общего члена. Формула 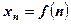позволяет вычислить любой член последовательности по номеру n, по ней можно сразу вычислить любой член последовательности. Так, равенства

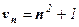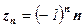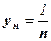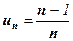, , , , n Î N

задают соответственно последовательности

; ;

; .

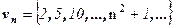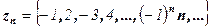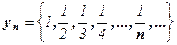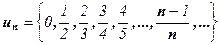Последовательность {х_n} называется ограниченной, если существует такое число М > 0, что для любого n Î Nвыполняется неравенство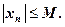

В противном случае последовательность называется неограниченной. Легко видеть, что последовательности у_n и u_n ограничены, а ν_n и z_n – неограничены.

Последовательность {х_n} называется возрастающей (неубывающей), если для любого n выполняется неравенство х_n+1 > х_n (х_n+1 ≥ х_n).

Аналогично определяется убывающая (невозрастающая) последовательность.

Все эти последовательности называются монотоннымипоследовательностями. Последовательности ν_n, у_n и u_n монотонные, а z_n – не монотонная.

Если все элементы последовательности {х_n} равны одному и тому же числу с, то ее называют постоянной.