Предел числовой последовательности
Число а называется пределом последовательности {хn}, если для любого положительного числа e найдется такое натуральное число N, что при всех n > N выполняется неравенство |xn - a| < e .
В этом случае пишут 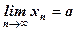 или хn → а при n →
или хn → а при n → 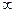 и говорят, что последовательность {хn} имеет предел, равный числу а (или хn стремится к а). Говорят также, что последовательность {хn} сходитсяк а.
и говорят, что последовательность {хn} имеет предел, равный числу а (или хn стремится к а). Говорят также, что последовательность {хn} сходитсяк а.
Коротко определение предела можно записать так:
("e > 0 $N: " n >N Þ |xn - a| < e) Û 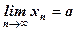 .
.
Геометрический смысл определения предела последовательности.
Неравенство |xn - a| < e равносильно неравенствам – ε < хn – а < ε
или а – ε < хn < а + ε, которые показывают, что элемент хn находится в
ε-окрестности точки а.
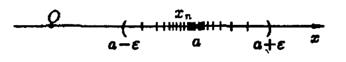
Поэтому определение предела последовательности геометрически можно сформулировать так:
Число а называется пределом последовательности {хn}, если для любой ε-окрестности точки а найдется натуральное число N, что все значения хn, для которых n > N, попадут в ε-окрестность точки а.
Ясно, что чем меньше ε, тем больше число N, но в любом случае внутри ε-окрестности точки а находится бесконечное число членов последовательности, а вне ее может быть лишь конечное их число.
Отсюда следует, что сходящаяся последовательность имеет только один предел. Последовательность, не имеющая предела, называется расходящейся. Таковой является, например, последовательность 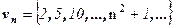 .
.
Постоянная последовательность хn = с, n Î N имеет предел, равный числу с, т.е. 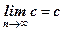 .
.
Дата добавления: 2014-12-05; просмотров: 4022;
