Односторонние пределы
В определении предела функции 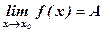 считается, что х стремится к х0 любым способом: оставаясь меньшим, чем x0 (слева от х0); большим, чем х0 (справа от х0); или колеблясь около точки x0.
считается, что х стремится к х0 любым способом: оставаясь меньшим, чем x0 (слева от х0); большим, чем х0 (справа от х0); или колеблясь около точки x0.
Бывают случаи, когда способ приближения аргумента х к х0 существенно влияет на значение предела функции. Поэтому вводят понятия односторонних пределов.
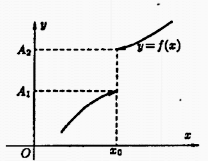
Число А1 называется пределом функции у = f(х) слева в точке х0, если для любого числа ε > 0 существует число δ = δ(ε) > 0 такое, что при х Î (x0 – δ; x0), выполняется неравенство 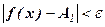 . Предел слева записывают так:
. Предел слева записывают так: 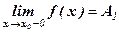 или коротко: f(х0 – 0) = А1 (обозначение Дирихле).
или коротко: f(х0 – 0) = А1 (обозначение Дирихле).
Аналогично определяется предел функции справа, запишем его с помощью символов:
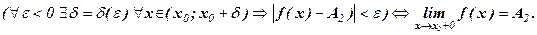
Коротко предел справа обозначают f(х0 + 0) = A2.
Пределы функции слева и справа называются одностороннимипределами. Очевидно, если существует 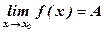 , то существуют и оба односторонних предела, причем А = А1 = А2.
, то существуют и оба односторонних предела, причем А = А1 = А2.
Справедливо и обратное утверждение:
если существуют оба предела f(х0 – 0) и f(х0 + 0) и они равны, то существует предел А = 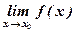 и А = f(х0 –0) = f(х0 + 0).
и А = f(х0 –0) = f(х0 + 0).
Если же А1 ≠ А2, то 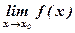 не существует.
не существует.
Предел функции при x → ¥
Пусть функция у = f(х) определена в промежутке (–¥; ¥).
Число А называется пределом функции f(х) при х → ¥, если для любого положительного числа ε существует такое число М = М(ε) > 0, что при всех х, удовлетворяющих неравенству |х| > М выполняется неравенство
| f(х) – А| < ε.
Записывают 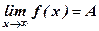 или f(х) → А при х → ¥.
или f(х) → А при х → ¥.
Коротко это определение можно записать так:
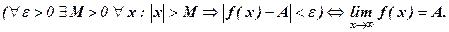
Если x → +¥, то пишут 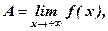 если x → –¥, то пишут
если x → –¥, то пишут 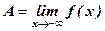 .
.
Геометрический смысл этого определения таков:
Для 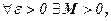 что при х Î (– ¥; –М) или х Î (M; + ¥) соответствующие значения функции f(х) попадают в ε-окрестность точки А, т.е. точки графика лежат в полосе шириной 2ε, ограниченной прямыми у = А + ε и у = А - ε.
что при х Î (– ¥; –М) или х Î (M; + ¥) соответствующие значения функции f(х) попадают в ε-окрестность точки А, т.е. точки графика лежат в полосе шириной 2ε, ограниченной прямыми у = А + ε и у = А - ε.
Бесконечна большая функция (б.б.ф.)
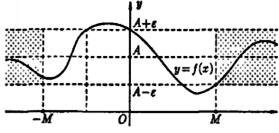
Функция у = f(х) называется бесконечно большой при х → х0, если для любого числа М>0 существует число δ=δ(М)>0, что для всех х≠х0, удовлетворяющих неравенству |х – х0|<δ, выполняется неравенство | f(x)| > M. Записывают 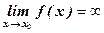 или f(х) → ¥ при х → х0.
или f(х) → ¥ при х → х0.
Коротко:
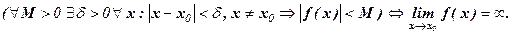
Например, функция у = 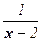 есть б.б.ф. при х → 2.
есть б.б.ф. при х → 2.
Если f(x) стремится к бесконечности при х → х0 и принимает лишь положительные значения, то пишут 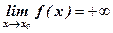 ; если лишь отрицательные значения, то
; если лишь отрицательные значения, то 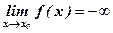 .
.
Функция у = f(х), заданная на всей числовой прямой, называется бесконечно большой при х → ¥, если для любого числа М > 0 найдется такое число N = N(М) > 0, что при всех х, удовлетворяющих неравенству |х| > N, выполняется неравенство | f(х) | > M. Коротко:
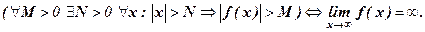
Например, у = 2х есть б.б.ф. при х → ¥.
Если аргумент х, стремясь к бесконечности, принимает лишь натуральные значения, т.е. х Î N, то соответствующая б.б.ф. становится бесконечно большой последовательностью. Например, последовательность 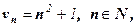 является бесконечно большой последовательностью. Очевидно, что всякая б.б.ф, в окрестности точки х0 являетсянеограниченнойв этой окрестности. Обратное утверждение неверно: неограниченная функция может и не быть б.б.ф. (Например, у = хsin х.)
является бесконечно большой последовательностью. Очевидно, что всякая б.б.ф, в окрестности точки х0 являетсянеограниченнойв этой окрестности. Обратное утверждение неверно: неограниченная функция может и не быть б.б.ф. (Например, у = хsin х.)
Однако, если 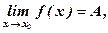 где А – конечное число, то функция f(х) ограничена в окрестности точки x0.
где А – конечное число, то функция f(х) ограничена в окрестности точки x0.
Бесконечно малые функции (б.м.ф.)
Функция у = f(х) называется бесконечно малой при х → х0, если
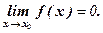
По определению предела функции это равенство означает: для любого числа ε > 0 найдется число δ > 0 такое, что для всех х, удовлетворяющих неравенству 0 < |х – х0| < δ, выполняемся неравенство | f(х)| < ε.
Аналогично определяется б.м.ф. при х → х0 + 0, x → х0 – 0, х → + ¥, х → – ¥ : во всех этих случаях f(х) → 0.
Бесконечно малые функции часто называют бесконечно малымивеличинамиили бесконечно малыми; обозначают обычно греческими буквами α, β и т. д.
Примерамиб.м.ф. служат функции у = х2 при х→0; у = х – 2 при х→2; у = sin x при х →  . Другой пример: хn =
. Другой пример: хn = 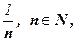 – бесконечно малая последовательность.
– бесконечно малая последовательность.
Теорема 1. Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
Теорема 2. Произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая.
Следствие 1. Так как всякая б.м.ф. ограничена, то из теоремы 2 вытекает: произведение двух б.м.ф. есть функция бесконечно малая.
Следствие 2. Произведение б.м.ф. на число есть функция бесконечно малая.
Теорема 3. Частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть функция бесконечно малая.
Теорема 4 (связь между бесконечно малыми и бесконечно большими функциями). Если функция a(х) – бесконечно малая (a ≠ 0), то функция – 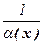 есть бесконечно большая функция и наоборот: если функция f(x) – бесконечно большая, то
есть бесконечно большая функция и наоборот: если функция f(x) – бесконечно большая, то 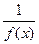 – бесконечно малая.
– бесконечно малая.
Теорема 5 (связь между функцией, ее пределоми бесконечно малой функцией). Если функция f(х) имеем предел, равный А, то ее можно представить как сумму числа А и бесконечно малой функции a(х), т.е. если 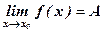 , то f(х) = А + a(х).
, то f(х) = А + a(х).
Теорема 6 (обратная).Если функцию f(х) можно представить в виде суммы числа А и бесконечно малой функции a(х), то число А является пределом функции f(х), т.е. если 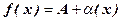 , то
, то 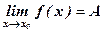 .
.
Дата добавления: 2014-12-05; просмотров: 1876;
