Прямая задача динамики точки
Если движение точки массой m задано координатным способом, значит, заданы кинематические уравнения движения точки в виде функций  . Дважды дифференцируя их по времени, находят проекции ускорений
. Дважды дифференцируя их по времени, находят проекции ускорений 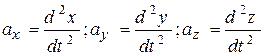 , с помощью дифференциальных уравнений движения находят проекции силы
, с помощью дифференциальных уравнений движения находят проекции силы 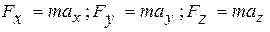 , по ним – модуль приложенной к точке силы
, по ним – модуль приложенной к точке силы  . Ее направление аналитически находят по направляющим косинусам (ч. 1, п. 1.2.2).
. Ее направление аналитически находят по направляющим косинусам (ч. 1, п. 1.2.2).
Если движение точки массой m задано естественным способом, значит, задан закон движения s = s(t) точки и известна траектория точки. В этом случае находят скорость 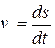 , касательное
, касательное  , нормальное ускорения
, нормальное ускорения 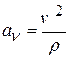 точки, с помощью дифференциальных уравнений движения находят проекции силы на касательную
точки, с помощью дифференциальных уравнений движения находят проекции силы на касательную 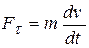 , главную нормаль
, главную нормаль 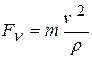 , по ним – модуль приложенной к точке силы
, по ним – модуль приложенной к точке силы 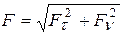 . Для определения соотношений между приложенными к точке силами иногда приходится использовать третье из дифференциальных уравнений движения в естественной форме:
. Для определения соотношений между приложенными к точке силами иногда приходится использовать третье из дифференциальных уравнений движения в естественной форме: 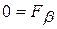 .
.
Дата добавления: 2014-12-01; просмотров: 1026;
