Законы динамики

Все содержание динамики строится на законах динамики (аксиомах, законах Ньютона).

Первый закон (закон инерции). Свободная материальная точка сохраняет состояние покоя или прямолинейного равномерного движения до тех пор, пока другие материальные объекты путем силового воздействия на точку не изменят этого состояния.

Свойство материальной точки сохранять свою скорость постоянной по направлению и величине (в том числе при покое – равной нулю) называется инертностью. Мерой инертности материальной точки является ее масса (п. 3.1.1).

Второй закон (основной закон динамики). Ускорение, получаемое материальной точкой от действия на нее силы, пропорционально модулю силы и направлено в сторону действия силы.

Математически этот закон выражается в виде основного уравнения динамики:

где - масса точки, - ускорение, получаемое точкой от действия на нее силы .

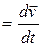Из основного уравнения динамики следует, что если сила на точку не действует ( = 0), то ускорение =0, скорость 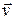точки остается постоянной по направлению и величине – точка движется прямолинейно и равномерно, в том числе может находиться в состоянии покоя ( 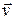= 0). Это значит, что основной закон динамики включает в себя как частный случай закон инерции.

Для свободной материальной точки, находящейся в поле сил тяжести, из основного уравнения динамики следует соотношение между массой и силой тяжести: 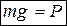, где g – ускорение свободного падения.

Первый и второй законы динамики справедливы только по отношению к абсолютному движению (ч. 2, п. 2.5.1, а также п. 3.8.3), по определению – в так называемых инерциальных системах отсчета. Для большинства практических задач за инерциальную можно принять систему отсчета (систему координат), связанную с вращающейся и фактически движущейся Землей.

Третий закон (закон равенства действия и противодействия). При действии одного материального объекта на другой возникает такое же по величине, противоположно направленное противодействие (ч. 1, п. 1.1.2).

Этот закон справедлив не только при взаимодействии соприкасающихся тел (для реакций связей, ч. 1, п. 1.1.3), но и в случае, когда взаимодействующие тела не касаются друг друга (для активных сил). В любом случае, так как силы действия и противодействия приложены к разным материальным объектам, они не образуют уравновешенной системы сил.

Четвертый закон (закон независимости действия сил). Ускорение материальной точки от действия на нее нескольких сил равно геометрической сумме ускорений, получаемых точкой от действия на нее каждой силы в отдельности.

Это означает, что основное уравнение динамики справедливо при действии на точку не только одной, а и нескольких сил: 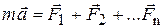, иначе 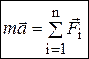, где n – число действующих на точку сил. В этом смысле последнее векторное равенство ничем не отличается от основного уравнения динамики, если в нем под силой подразумевать геометрическую сумму всех сил, действующих на точку: .