Дифференциальные уравнения движения точки

Из кинематики известно (ч. 2, п. 2.2.3), что ускорение точки через ее радиус-вектор 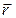выражается так: 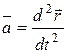. Тогда из основного уравнения динамики получим дифференциальное уравнение движения точки в векторной форме: 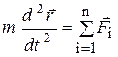или .

В проекциях на оси заранее выбранной прямоугольной системы координат xyz из основного уравнения динамики получают дифференциальные уравнения движения в координатной форм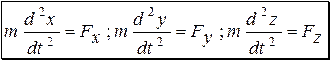е: , где - суммы проекций всех сил, действующих на точку, на соответствующую ось.

В проекциях на естественные оси (касательная), (главная нормаль) и (бинормаль, ч. 2, п. 2.2.4) получают дифференциальные уравнения движения в естественной форме: . Здесь v – модуль скорости, 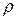- радиус кривизны траектории, - суммы проекций всех сил, действующих на точку, соответственно: на касательную , главную нормаль и бинормаль .